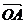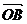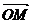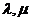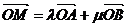2）显然与可作为平面向量的一组基底，由平面向量基本定理，对于这一平面内的向量，有且只有一对实数，使得等式成立。设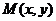，由1）中各点的坐标有：

所以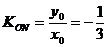，即为所求。                                    ………5分

设，弦AB的中点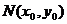，由③及韦达定理有：

由①，②有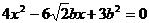：         ③

据题意有AB所在的直线方程为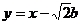：   ②                     ………3分

易知右焦点F的坐标为（），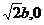

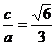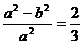20．解：  1）设椭圆的焦距为2c,因为，所以有，故有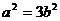。从而椭圆C的方程可化为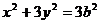：      ①                     ………2分

当且仅当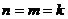时取“＝”。                                     ………13分

综上可知：若正整数n, m, k成等差数列，不等式 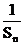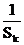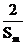＋≥总成立。