
1.(本小题满分10分)一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=2.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)点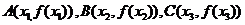 从左到右依次是函数
从左到右依次是函数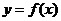 图象上三点,其中
图象上三点,其中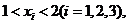 求证:ㄓ
求证:ㄓ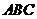 是钝角三角形.
是钝角三角形.
第Ⅱ部分 加试内容
(命题单位:通州中学 满分40分,答卷时间30分钟)
(1)试求函数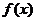 的单调区间;
的单调区间;
20.对于函数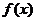 ,若存在
,若存在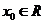 ,使
,使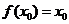 成立,则称
成立,则称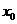 为
为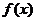 的不动点。如果函数
的不动点。如果函数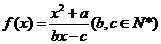 有且仅有两个不动点
有且仅有两个不动点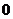 、
、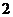 ,且
,且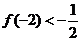 。
。
⑵ 设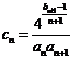 ,证明:
,证明: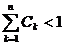 .
.
⑴ 判断数列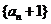 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
19.(本题满分16分)已知数列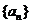 的首项
的首项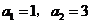 ,前
,前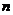 项和为
项和为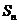 ,且
,且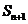 、
、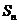 、
、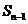 (n ≥2)分别是直线
(n ≥2)分别是直线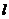 上的点A、B、C的横坐标,
上的点A、B、C的横坐标,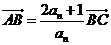 ,设
,设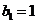 ,
,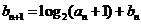 .
.
(2)若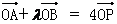 ,求m的取值范围.
,求m的取值范围.
18.(本题满分15分)椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且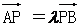 .
.
(1)求椭圆方程;
(2)求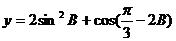 的值域.
的值域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com