F (x)＝a ^x－x(a＞1)的单调性可知：-∞＜0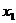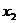＜＜＜＜+∞，这说明函数f (x)＝a ^x (a＞1)的图像与直线y＝x有两不同的公共点个公共点。      ………12分

综上所述：

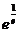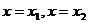当a＜时：F (x)_min ＝F ()＜0，所以方程F (x)＝a ^x－x ＝0有两相异的实数解（设＜)。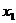

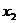又因为当x → -∞或x → +∞时有F (x) → +∞，且F (0)＝1，所以据函数

  当a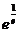＝时：F (x)_min ＝F ()＝F (e)＝0，所以方程F (x)＝a ^x－x ＝0有唯一实数解x ＝＝e。这说明函数f (x)＝a ^x (a＞1)的图像与直线y＝x有唯一公共点；                                                     ………11分

故当a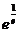＞时：F (x)_min ＝F ()＞0，所以方程F (x)＝a ^x－x ＝0无实数解，这说明函数f (x)＝a ^x (a＞1)的图像与直线y＝x没有公共点；           ………10分

令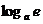－＞0，解得：a ＞。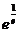

所以F (x)的最小值为F (x)_min＝F ()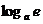＝－。………9分

当x ≤时：F′ (x)≤0，F (x)在区间上是减函数。

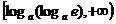所以当x ≥时：F′ (x)≥0，F (x)在区间上是增函数；

解得：x ≥。

21．解； 1）设点M（x₀, y₀）是函数y ＝ f (x)的图像与其反函数y ＝ f ^-1 (x)的图像的公

点，则有：y₀＝f (x₀) ，                                    

y₀ ＝ f ^-1 (x₀)，据反函数的意义有：x₀ ＝ f (y₀)。                        ………2分

所以：y₀ ＝ f (x₀)且同时有x₀ ＝ f (y₀)。

若x₀ ＜ y₀ ，因为函数y ＝ f (x) 是其定义域上是增函数，

所以有：f (x₀) ＜ f (y₀) ，即y₀ ＜ x₀ 与 x₀ ＜ y₀矛盾，这说明x₀ ＜ y₀是错误的。

同理可证x₀ ＞ y₀也是错误的。

所以x₀ ＝ y₀ ，即函数y ＝ f (x)的图像与其反函数y ＝ f ^-1 (x)的图像有公共点在直线y ＝ x上；                                                        ………5分

2）构造函数F (x)＝a ^x－x(a＞1)

因为F′ (x)＝ a ^xlna － 1（a ＞ 1），                               ………6分

令F′ (x)＝ a ^xlna － 1≥0，