
5.双曲线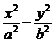 =1的实轴为A1A2,点P是双曲线上的一个动点,引A1Q⊥A1P,A2Q⊥A2P,A1Q与A2Q的交点为Q,求Q点的轨迹方程.
=1的实轴为A1A2,点P是双曲线上的一个动点,引A1Q⊥A1P,A2Q⊥A2P,A1Q与A2Q的交点为Q,求Q点的轨迹方程.
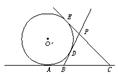
4.已知A、B、C是直线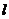 上的三点,且|AB|=|BC|=6,⊙O′切直线
上的三点,且|AB|=|BC|=6,⊙O′切直线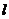 于点A,又过B、C作⊙O′异于
于点A,又过B、C作⊙O′异于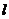 的两切线,设这两切线交于点P,求点P的轨迹方程.
的两切线,设这两切线交于点P,求点P的轨迹方程.
3.设直线2x-y-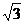 =0与y轴的交点为P,点P把圆(x+1)2+y2 =25的直径分为两段,则其长度之比是
=0与y轴的交点为P,点P把圆(x+1)2+y2 =25的直径分为两段,则其长度之比是
2.高为5 m和3 m的两根旗杆竖在水平地面上,且相距10 m,如果把两旗杆底部的坐标分别确定为A(-5,0)、B(5,0),则地面观测两旗杆顶端仰角相等的点的轨迹方程是_________.
1.已知椭圆的焦点是F1、F2,P是椭圆上的一个动点,如果延长F1P到Q,使得|PQ|=|PF2|,那么动点Q的轨迹是( )
A.圆 B.椭圆
C.双曲线的一支 D.抛物线
[例1]如图所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程.
解:设AB的中点为R,坐标为(x,y),则在Rt△ABP中,|AR|=|PR|.
又因为R是弦AB的中点,依垂径定理:在Rt△OAR中,|AR|2=|AO|2-|OR|2=36-(x2+y2)
又|AR|=|PR|=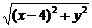
所以有(x-4)2+y2=36-(x2+y2),即x2+y2-4x-10=0
因此点R在一个圆上,而当R在此圆上运动时,Q点即在所求的轨迹上运动.
设Q(x,y),R(x1,y1),因为R是PQ的中点,所以x1=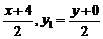 ,
,
代入方程x2+y2-4x-10=0,得
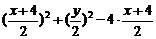 -10=0
-10=0
整理得 x2+y2=56,这就是所求的轨迹方程.
技巧与方法:对某些较复杂的探求轨迹方程的问题,可先确定一个较易于求得的点的轨迹方程,再以此点作为主动点,所求的轨迹上的点为相关点,求得轨迹方程.
[例2]某检验员通常用一个直径为2 cm和一个直径为1 cm的标准圆柱,检测一个直径为3 cm的圆柱,为保证质量,有人建议再插入两个合适的同号标准圆柱,问这两个标准圆柱的直径为多少?
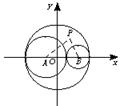 解:设直径为3,2,1的三圆圆心分别为O、A、B,问题转化为求两等圆P、Q,使它们与⊙O相内切,与⊙A、⊙B相外切.
解:设直径为3,2,1的三圆圆心分别为O、A、B,问题转化为求两等圆P、Q,使它们与⊙O相内切,与⊙A、⊙B相外切.
建立如图所示的坐标系,并设⊙P的半径为r,则
|PA|+|PO|=1+r+1.5-r=2.5
∴点P在以A、O为焦点,长轴长2.5的椭圆上,其方程为
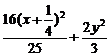 =1
①
=1
①
同理P也在以O、B为焦点,长轴长为2的椭圆上,其方程为
(x-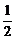 )2+
)2+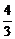 y2=1
②
y2=1
②
由①、②可解得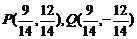 ,∴r=
,∴r=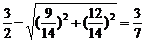
故所求圆柱的直径为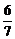 cm.
cm.
[例3] 直线L: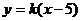 与圆O:
与圆O: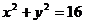 相交于A、B两点,当k变动时,弦AB的中点M的轨迹方程.
相交于A、B两点,当k变动时,弦AB的中点M的轨迹方程.
错解:易知直线恒过定点P(5,0),再由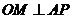 ,得:
,得:

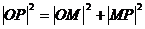
∴
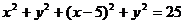 ,整理得:
,整理得:
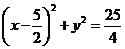
分析:求动点轨迹时应注意它的完备性与纯粹性。本题中注意到点M应在圆内,故易求得轨迹为圆内的部分,此时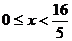 .
.
[例4]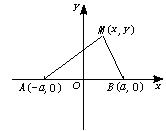 已知A、B为两定点,动点M到A与到B的距离比为常数λ,求点M的轨迹方程,并注明轨迹是什么曲线.
已知A、B为两定点,动点M到A与到B的距离比为常数λ,求点M的轨迹方程,并注明轨迹是什么曲线.
解:建立坐标系如图所示,
设|AB|=2a,则A(-a,0),B(a,0).
设M(x,y)是轨迹上任意一点.
则由题设,得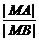 =λ,坐标代入,得
=λ,坐标代入,得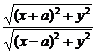 =λ,化简得
=λ,化简得
(1-λ2)x2+(1-λ2)y2+2a(1+λ2)x+(1-λ2)a2=0
(1)当λ=1时,即|MA|=|MB|时,点M的轨迹方程是x=0,点M的轨迹是直线(y轴).
(2)当λ≠1时,点M的轨迹方程是x2+y2+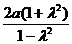 x+a2=0.点M的轨迹是以
x+a2=0.点M的轨迹是以
(-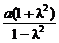 ,0)为圆心,
,0)为圆心,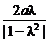 为半径的圆.
为半径的圆.
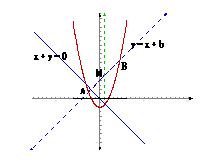
[例5]若抛物线y=ax2-1上,总存在不同的两点A、B关于直线y+x=0对称,求实数a的取值范围.
分析:若存在A、B关于直线y+x=0对称,A、B必在与直线y+x=0垂直的直线系中某一条与抛物线y=ax2-1相交的直线上,并且A、B的中点M恒在直线y+x=0上.
解:如图所示,设与直线y+x=0垂直的直线系方程为
y=x+b
 由
由
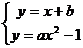 得
得
ax2-x-(b+1)=0 ①
令 △>0
即 (-1)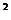 -4a[-(b+1)]>0
-4a[-(b+1)]>0
整理得
4ab+4a+1>0 ②
在②的条件下,由①可以得到直线y=x+b、抛物线y=ax2-1的交点A、B的中点M的坐标为
(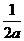 ,
,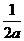 +b),要使A、B关于直线y+x=0对称,则中点M应该在直线y+x=0上,所以有
+b),要使A、B关于直线y+x=0对称,则中点M应该在直线y+x=0上,所以有
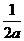 +(
+(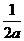 +b)=0 ③
+b)=0 ③
即 b=-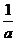 代入②解不等式得
a>
代入②解不等式得
a>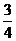
因此,当a>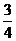 时,抛物线y=ax2-1上总存在不同的两点A、B关于直线y+x=0对称.
时,抛物线y=ax2-1上总存在不同的两点A、B关于直线y+x=0对称.
3.在求轨迹问题时常用的数学思想是:
(1)函数与方程的思想:求平面曲线的轨迹方程,是将几何条件(性质)表示为动点坐标x、y的方程及函数关系;
(2)数形结合的思想:由曲线的几何性质求曲线方程是“数”与“形”的有机结合;
(3)等价转化的思想:通过坐标系使“数”与“形”相互结合,在解决问题时又需要相互转化.
2.求轨迹方程的基本方法有:
(1)直接法:若动点满足的几何条件是一些几何量的等量关系,则将这些关系“翻译”成x,y的关系式,由此得到轨迹方程.一般步骤是:建立坐标系-设点-列式-代换-化简、整理.
(2)定义法:即当动点的轨迹满足的条件符合某种特殊曲线的定义时,则可根据这种曲线的定义建立方程.
(3)待定系数法:已知动点的轨迹是某种圆锥曲线,则可先设出含有待定系数的方程,再根据动点满足的条件确定待定系数.
(4)相关点法:当动点P(x,y)随着另一动点Q(x1,y1)的运动而运动时,而动点Q在某已知曲线上,且Q点的坐标可用P点的坐标来表示,则可代入动点Q的方程中,求得动点P的轨迹方程.
(5)参数法:当动点P的坐标x、y之间的直接关系不易建立时,可适当地选取中间变量t,并用t表示动点的坐标x、y,从而得到动点轨迹的参数方程 ,消去t,便可得动点P的普通方程.
另外,还有交轨法、几何法等.
1.在求曲线轨迹方程的过程中,要注意:
(1)理解题意,弄清题目中的已知和结论,发现已知和未知的关系,进行知识的重新组合;
(2)合理进行数学语言间的转换,数学语言包括文字语言、符号语言和图形语言,通过审题画出必要的图形或示意图,把不宜于直接计算的关系化为能直接进行数学处理的关系式,把不便于进行数学处理的语言化为便于数学处理的语言;
(3)注意挖掘题目中的隐含条件;
(4)注意反馈和检验.
4.坐标变换
(1)坐标变换 在解析几何中,把坐标系的变换(如改变坐标系原点的位置或坐标轴的方向)叫做坐标变换.实施坐标变换时,点的位置,曲线的形状、大小、位置都不改变,仅仅只改变点的坐标与曲线的方程.坐标轴的平移:坐标轴的方向和长度单位不改变,只改变原点的位置,这种坐标系的变换叫做坐标轴的平移,简称移轴.
(2)坐标轴的平移公式 设平面内任意一点M,它在原坐标系xOy中的坐标是(x,y),在新坐标系x ′O′y′中的坐标是(x′,y′).设新坐标系的原点O′在原坐标系xOy中的坐标是(h,k),则
(1)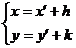 或 (2)
或 (2)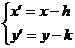
公式(1)或(2)叫做平移(或移轴)公式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com