
3、蜡块的位移
在直线运动中我们要确定物体运动的位移,我们只要知道物体的初末位置就可以了对于曲线运动也是一样的。在前面建立坐标系的时候我们已经说过了,物体开始运动的位置为坐标原点,现在我们要找任意时刻的位移,只要再找出任意时刻t物体所在的位置就可以了。
实际上这个问题我们已经解决了,前面我们已经找出物体在任意时刻的位置P(x,y),请同学们想一下在坐标中物体位移应该是怎么表示的呢?
在坐标系中,线段OP的长度就代表了物体位移的大小。现在我找一位同学来计算一下这个长度。
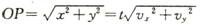
我们在前面的学习中已经知道位移是矢量,所以我们要计算物体的位移仅仅知道位移的大小是不够的,我们还要再计算位移的方向。这应该怎样来求呢?
因为坐标系中的曲线就代表了物体运动的轨迹,所以我们只要求出该直线与x轴的夹角θ就可以了。要求"我们只要求出它的正切就可以了。
tanθ==vy /vx
这样就可以求出θ,从而得知位移的方向。
现在我们已经知道了蜡块做的是直线运动,并且求出了蜡块在任意时刻的位移,但我们还不知道蜡块做的是什么样的直线运动,要解决这个问题,我们还需要求出蜡块的速度。
2、蜡块的运动轨迹
我们在数学课上就已经学过了怎样在坐标中表示一条直线或曲线。在数学上,关于x、y两个变量的方程就可以代表一条直线或曲线,现在我们要找的蜡块运动的轨迹,实际上我们只要找到表示蜡块运动轨迹的方程就可以了。观察我们刚才得到的关于蜡块位置的两个方程,发现在这两个关系式中,除了x、y之外还有一个变量“那我们应该如何来得到蜡块的轨迹方程呢?
根据数学上的消元法,我们可以从这两个关系式中消去变量t,就可以得到关于x,y两个变量的方程了。实际上我们前面得到的两个关系式就相当于我们在数学上学到的参数方程,消t的过程实际上就是消参数的过程。
那消参数的过程和结果应该是怎样的呢?
我们可以先从公式(1)中解出t
t=x/vx y=vy x/vx
现在我们对公式④进行数学分析,看看它究竟代表的是一条什么样的曲线呢?
由于蜡块在x、y两个方向上做的都是匀速直线运动,所以vy 、vx都是常量.所以vy /vx也是常量,可见公式④表示的是一条过原点的倾斜直线。
在物理上这代表什么意思呢?
这也就是说,蜡块相对于黑板的运动轨迹是直线,即蜡块做的是直线运动。
既然这个方程所表示的直线就是蜡块的运动轨迹,那如果我们要找靖块在任意时刻的位移,是不是就可以通过这条直线来实现呢?下面我们就来看今天的第三个问题。
我们先来回想一下我们是怎样研究直线运动的,同学们可以从如何确定质点运动的位移来考虑。
可以沿着物体或质点运动的轨迹建立直线坐标系,通过物体或质点坐标的变化可以确定其位移,从而达到研究物体运动过程的目的。现在我们先看一个匀加速直线运动的例子。

物体运动轨迹是直线,位移增大的越来越快,初逮度为零,速度均匀增大,加速度保持不变,所以这种运动为初速度为零的匀加速直线运动。
现在我们可以看到,我们已经把这个物体的运动分解成了两个运动:其一是速度为vO的匀速直线运动:其二是同方向的初速度为0,加速度为a的匀加速直线运动。可以说这种方法可以将比较复杂的一个运动运动转化成两个或几个比较简单的运动,这种方法我们称为运动的分解。实际上运动的分解不仅能够应用在直线运动中,对于曲线运动它同样适用。下面我们就来探究一下怎样应用运动的合成与分解来研究曲线运动。
演示实验:如图6.2-l所示,在一端封闭、长约l m的玻璃管内注满清水,水中放一红蜡做的小圆柱体R,将玻璃管的开口端用胶塞塞紧。(图甲)
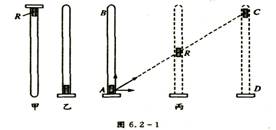
将这个玻璃管倒置(图乙),蜡块R就沿玻璃管上,如果旁边放一个米尺,可以看到蜡块上升的速度大致不变,即蜡块做匀连直线运动。
再次将玻璃管上下颠倒,在蜡块上升的同时将玻璃管水平向右匀速移动,观察蜡块的运动。(图丙)
在黑板的背景前观察由甲到乙的过程,可以发现蜡块做的是匀速直线运动,而过程丙中蜡块微的是什么运动呢?有可能是直线运动,速度大小变不变化不能判断,有可能是曲线运动。也就是说,仅仅通过用眼睛观察我们并不能得到物体运动的准确信息,要精确地了解物体的运动过程,还需要我们进行理论上的分析。下面我们就通过运动的分解对该物体的运动过程进行分析。
对于直线运动,很明显,其运动轨迹就是直线,直接建立直线坐标系就可以解决问题,但如果是一个运动轨迹不确定的运动还能这样处理吗?很显然是不能的,这时候我们可以选择平面内的坐标系了。比如选择我们最熟悉的平面直角坐标系。下面我们就来看一看怎样在乎面直角坐标系中研究物体的运动。
1、蜡块的位置
建立如图6.2-2所示的平面直角坐标系:选蜡块开始运动的位置为原点,水平向右的方向和竖直向上的方向分别为x轴和y轴的正方向。
在观察中我们已经发现蜡块在玻璃管中是匀速上升的,所以我们设蜡块匀速上升的速度为vy,玻璃管向右匀速运动的速度为vx,从蜡块开始运动的时刻开始计时,我们就可以得到蜡块在t时刻的位置P(x,y),我们该如何得到点p的两个坐标呢?
蜡块在两个方向上做的都是匀速直线运动,所以x、y可以通过匀速直线运动的位移公式x=vt获得,即:
x=vxt y=vyt
这样我们就确定了蜡块运动过程中任意时刻的位置,然而要知道蜻块做的究竟是什么运动这还不够,我们还要知道蜡块的运动轨迹是什么样的。下面我们就来操究这个问题。
上节课我们学习了曲线运动的定义,性质及物体做曲线运动的条件,先来回顾一下这几个问题:什么是曲线运动?(运动轨迹是曲线的运动是曲线运动。)
怎样确定做曲线运动的物体在某一时刻的速度方向?(质点在某一点的速度方向沿曲线在这一点的切线方向。)
物体在什么情况下做曲线运动?(当物体所受合力的方向跟它的速度方向不在同一直线上时,物体做曲线运动。)
通过上节课的学习,我们对曲线运动有了一个大致的认识,但我们还投有对曲线运动进行深入的研究,要研究曲线运动需要什么样的方法呢?这节课我们就来研究这个问题。
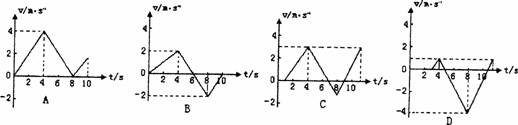
5.A、B、C、D四个物体做直线运动的速度图象如图示,以向东为正方向,由图看出 __________物体在10s内是往返运动,且lOs末在出发点的东边;_________物体在10s末在出发点的西边;_________物体只向东运动,速度方向不变。
4.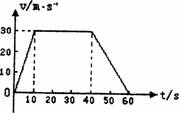 如图所示,是一个物体向东运动的速度图象,由图可知0-10s内物体的加速度大小是________,方向是___________ ;在10s-40s内物体的加速度大小是_______;在40s-60s内物体的加速度大小是___________,方向是____________ 。
如图所示,是一个物体向东运动的速度图象,由图可知0-10s内物体的加速度大小是________,方向是___________ ;在10s-40s内物体的加速度大小是_______;在40s-60s内物体的加速度大小是___________,方向是____________ 。
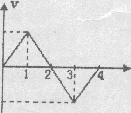
3.如图示,是一质点从位移原点出发的v--t图象,下列说法正确
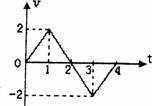 的是( )
的是( )
A. 1s末质点离开原点最远
B.2S末质点回到原点
C.3s末质点离开原点最远
D.4s末质点回到原点
2.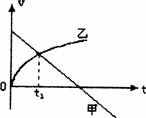 甲、乙两物体的v--t图象如图所示,下列判断正确的是( )
甲、乙两物体的v--t图象如图所示,下列判断正确的是( )
A. 甲作直线运动,乙作曲线运动
B.tl时刻甲乙相遇


C.tl时间内甲的位移大于乙的位移






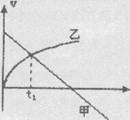

D.tl时刻甲的加速度大于乙的加速度
1. 关于直线运动的位移、速度图象,下列说法正确的是( )
A、 匀速直线运动的速度-时间图象是一条与时间轴平行的直线
B、 匀速直线运动的位移-时间图象是一条与时间轴平行的直线
C、 匀变速直线运动的速度-时间图象是一条与时间轴平行的直线
D、 非匀变速直线运动的速度-时间图象是一条倾斜的直线
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com