
1.从长方体一个顶点出发的三个面的面积分别为6,8,12,则其对角线的长为
(A)3
(B)5 (C) 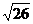 (D)
(D)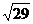
3.突出重点
综合考查在知识与方法的交汇点处设计命题,在不等式问题中蕴含着丰富的函数思想,不等式又为研究函数提供了重要的工具,不等式与函数既是知识的结合点,又是数学知识与数学方法的交汇点,因而在历年高考题中始终是重中之重。在全面考查函数与不等式基础知识的同时,将不等式的重点知识以及其他知识有机结合,进行综合考查,强调知识的综合和知识的内在联系,加大数学思想方法的考查力度,是高考对不等式考查的又一新特点。
2.强化不等式的应用
突出不等式的知识在解决实际问题中的应用价值,借助不等式来考查学生的应用意识。
高考中除单独考查不等式的试题外,常在一些函数、数列、立体几何、解析几何和实际应用问题的试题中涉及不等式的知识,加强不等式应用能力,是提高解综合题能力的关键.因此,在复习时应加强这方面训练,提高应用意识,总结不等式的应用规律,才能提高解决问题的能力。
如在实际问题应用中,主要有构造不等式求解或构造函数求函数的最值等方法,求最值时要注意等号成立的条件,避免不必要的错误。
1.在复习不等式的解法时,加强等价转化思想的训练与复习
解不等式的过程是一个等价转化的过程,通过等价转化可简化不等式(组),以快速、准确求解。
加强分类讨论思想的复习.在解不等式或证不等式的过程中,如含参数等问题,一般要对参数进行分类讨论.复习时,学生要学会分析引起分类讨论的原因,合理的分类,做到不重不漏。
加强函数与方程思想在不等式中的应用训练。不等式、函数、方程三者密不可分,相互联系、互相转化.如求参数的取值范围问题,函数与方程思想是解决这类问题的重要方法.在不等式的证明中,加强化归思想的复习,证不等式的过程是一个把已知条件向要证结论的一个转化过程,既可考查学生的基础知识,又可考查学生分析问题和解决问题的能力,正因为证不等式是高考考查学生代数推理能力的重要素材,复习时应引起我们的足够重视.
题型1:简单不等式的求解问题
例1.(福建省福州市普通高中09年高三质量检查)已知
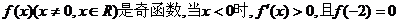 ,则不等式
,则不等式 
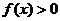 的解集是 ( )
的解集是 ( )
A.(-2,0) B.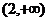

C.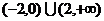 D.
D.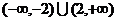

答案 C 
8.如果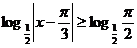 那么
那么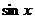 的取值范围是_______。
的取值范围是_______。
答案: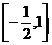

解析:因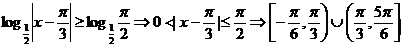

故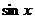
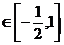

易错警示:利用真数大于零得x不等于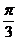 ,从而正弦值就不等于
,从而正弦值就不等于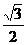 .其实x等于
.其实x等于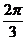 时可取得该值。
时可取得该值。
例2.同学们都知道,在一次考试后,如果按顺序去掉一些高分,那么班级的平均分将降低;
反之,如果按顺序去掉一些低分,那么班级的平均分将提高. 这两个事实可以用数学语
言描述为:若有限数列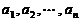 满足
满足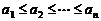 ,则
,则

(结论用数学式子表示).
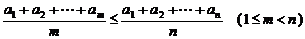 和
和
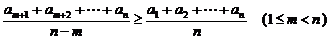

8.线性规划
(1)平面区域
一般地,二元一次不等式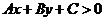 在平面直角坐标系中表示
在平面直角坐标系中表示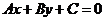 某一侧所有点组成的平面区域。我们把直线画成虚线以表示区域不包括边界直线。当我们在坐标系中画不等式
某一侧所有点组成的平面区域。我们把直线画成虚线以表示区域不包括边界直线。当我们在坐标系中画不等式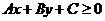 所表示的平面区域时,此区域应包括边界直线,则把直线画成实线.
所表示的平面区域时,此区域应包括边界直线,则把直线画成实线.
说明:由于直线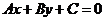 同侧的所有点的坐标
同侧的所有点的坐标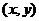 代入
代入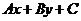 ,得到实数符号都相同,所以只需在直线某一侧取一个特殊点
,得到实数符号都相同,所以只需在直线某一侧取一个特殊点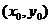 ,从
,从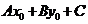 的正负即可判断
的正负即可判断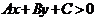 表示直线哪一侧的平面区域。特别地,当
表示直线哪一侧的平面区域。特别地,当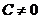 时,通常把原点作为此特殊点.
时,通常把原点作为此特殊点.
(2)有关概念
 引例:设
引例:设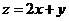 ,式中变量
,式中变量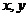 满足条件
满足条件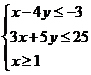 ,求
,求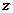 的最大值和最小值。
的最大值和最小值。
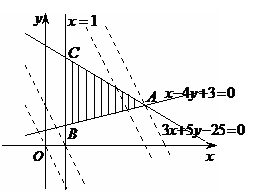
由题意,变量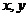 所满足的每个不等式都表示一个平面区域,不等式组则表示这些平面区域的公共区域。由图知,原点
所满足的每个不等式都表示一个平面区域,不等式组则表示这些平面区域的公共区域。由图知,原点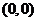 不在公共区域内,当
不在公共区域内,当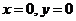 时,
时,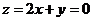 ,即点
,即点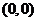 在直线
在直线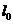 :
: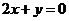 上,作一组平行于
上,作一组平行于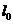 的直线
的直线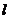 :
: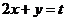 ,
,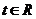 ,可知:当
,可知:当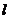 在
在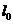 的右上方时,直线
的右上方时,直线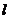 上的点
上的点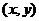 满足
满足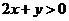 ,即
,即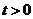 ,而且,直线
,而且,直线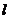 往右平移时,
往右平移时,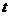 随之增大。
随之增大。
由图象可知,当直线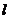 经过点
经过点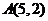 时,对应的
时,对应的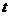 最大,
最大,
当直线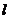 经过点
经过点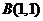 时,对应的
时,对应的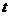 最小,所以,
最小,所以,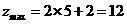 ,
,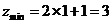 。
。
在上述引例中,不等式组是一组对变量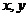 的约束条件,这组约束条件都是关于
的约束条件,这组约束条件都是关于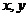 的一次不等式,所以又称为线性约束条件。
的一次不等式,所以又称为线性约束条件。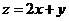 是要求最大值或最小值所涉及的变量
是要求最大值或最小值所涉及的变量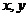 的解析式,叫目标函数。又由于
的解析式,叫目标函数。又由于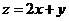 是
是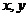 的一次解析式,所以又叫线性目标函数。
的一次解析式,所以又叫线性目标函数。
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题。满足线性约束条件的解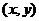 叫做可行解,由所有可行解组成的集合叫做可行域。在上述问题中,可行域就是阴影部分表示的三角形区域。其中可行解
叫做可行解,由所有可行解组成的集合叫做可行域。在上述问题中,可行域就是阴影部分表示的三角形区域。其中可行解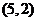 和
和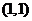 分别使目标函数取得最大值和最小值,它们都叫做这个问题的最优解.
分别使目标函数取得最大值和最小值,它们都叫做这个问题的最优解.
7.对数不等式
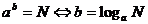

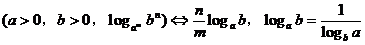 等,
等,
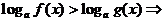

(1)当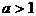 时,
时,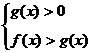 ;
;
(2)当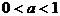 时,
时,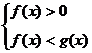 。
。
6.指数不等式
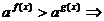

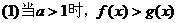 ;
;
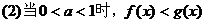 ;
;
5.简单的绝对值不等式
绝对值不等式适用范围较广,向量、复数的模、距离、极限的定义等都涉及到绝对值不等式。高考试题中,对绝对值不等式从多方面考查。
解绝对值不等式的常用方法:
①讨论法:讨论绝对值中的式于大于零还是小于零,然后去掉绝对值符号,转化为一般不等式;
②等价变形:
解绝对值不等式常用以下等价变形:
|x|<a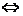 x2<a2
x2<a2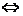 -a<x<a(a>0),
-a<x<a(a>0),
|x|>a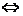 x2>a2
x2>a2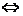 x>a或x<-a(a>0)。
x>a或x<-a(a>0)。
一般地有:
|f(x)|<g(x)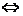 -g(x)<f(x)<g(x),
-g(x)<f(x)<g(x),
|f(x)|>g(x)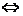 f(x)>g (x)或f(x)<g(x)。
f(x)>g (x)或f(x)<g(x)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com