
2. 解不等式
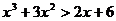

1.解不等式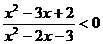

[例1] 如果kx2+2kx-(k+2)<0恒成立,则实数k的取值范围是___.
A. -1≤k≤0 B. -1≤k<0 C. -1<k≤0 D. -1<k<0
错解:由题意: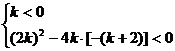

解得:-1<k<0
错因:将kx2+2kx-(k+2)<0看成了一定是一元二次不等式,忽略了k=0的情况.
正解:当k=0时,原不等式等价于-2<0,显然恒成立, k=0符合题意.
k=0符合题意.
当k 0时,由题意:
0时,由题意: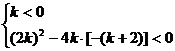

解得:-1<k<0
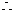
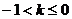 ,故选C.
,故选C.
[例2] 命题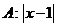 <3,命题
<3,命题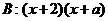 <0,若A是B的充分不必要条件,则
<0,若A是B的充分不必要条件,则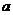 的取值范围是_______
的取值范围是_______
A.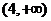 B.
B.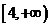 C.
C.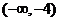 D.
D.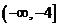

错解:由|x-1|<3得:-2<x<4,
又由(x+2)(x+a)=0得x=-2或x=-a,
 A是B的充分不必要条件,
A是B的充分不必要条件,
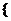 x|-2<x<4
x|-2<x<4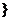
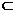
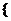 x|-2<x<-a
x|-2<x<-a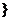

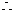 -a>4故选D.
-a>4故选D.
错因:忽略了a=-4时,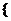 x|-2<x<4
x|-2<x<4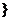 =
=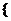 x|-2<x<-a
x|-2<x<-a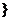 ,此时A是B的充要条件,不是充分不必要条件.
,此时A是B的充要条件,不是充分不必要条件.
正解:由|x-1|<3得:-2<x<4,
又由(x+2)(x+a)=0得x=-2或x=-a,
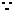 A是B的充分不必要条件,
A是B的充分不必要条件,
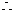
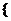 x|-2<x<4
x|-2<x<4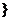
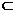
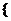 x|-2<x<-a
x|-2<x<-a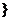

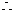 -a>4故选C.
-a>4故选C.
[例3]已知f(x) = ax + ,若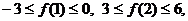 求
求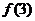 的范围.
的范围.
错解: 由条件得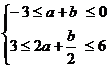


②×2-① 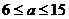
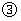

①×2-②得 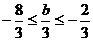
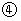

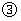 +
+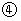 得
得 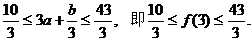

错因:采用这种解法,忽视了这样一个事实:作为满足条件的函数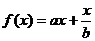 ,其值是同时受
,其值是同时受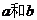 制约的.当
制约的.当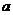 取最大(小)值时,
取最大(小)值时,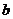 不一定取最大(小)值,因而整个解题思路是错误的.
不一定取最大(小)值,因而整个解题思路是错误的.
正解: 由题意有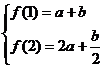 ,
,
解得: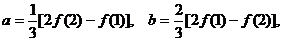

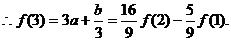 把
把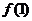 和
和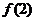 的范围代入得
的范围代入得 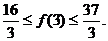

[例4] 解不等式(x+2)2(x+3)(x-2)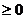

错解: (x+2)2
(x+2)2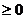

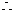 原不等式可化为:(x+3)(x-2)
原不等式可化为:(x+3)(x-2)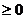

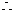 原不等式的解集为{x| x
原不等式的解集为{x| x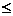 -3或x
-3或x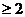 }
}
错因:忽视了“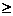 ”的含义,机械的将等式的运算性质套用到不等式运算中.
”的含义,机械的将等式的运算性质套用到不等式运算中.
正解:原不等式可化为:(x+2)2(x+3)(x-2)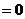 ①或(x+2)2(x+3)(x-2)
①或(x+2)2(x+3)(x-2)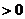 ②,
②,
解①得:x=-3或x=-2或x=2
解②得:x< -3或x>2
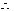 原不等式的解集为{x| x
原不等式的解集为{x| x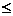 -3或x
-3或x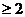 或x
或x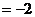 }
}
[例5] 解关于x的不等式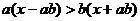

解:将原不等式展开,整理得: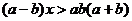

讨论:当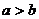 时,
时,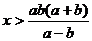

当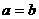 时,若
时,若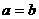 ≥0时
≥0时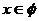 ;若
;若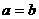 <0时
<0时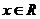

当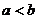 时,
时,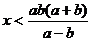

点评:在解一次不等式时,要讨论一次项系数的符号.
[例6]关于x的不等式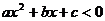 的解集为
的解集为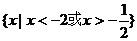

求关于x的不等式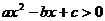 的解集.
的解集.
解:由题设知 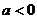 ,且
,且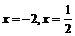 是方程
是方程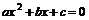 的两根
的两根
∴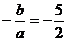 ,
, 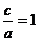

从而 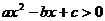 可以变形为
可以变形为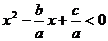

即: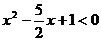 ∴
∴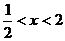

点评:二次不等式的解集与二次方程的根之间的联系是解本题的关健,这也体现了方程思想在解题中的简单应用.
[例7]不等式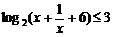 的解集为
的解集为 
解:∵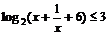 ,∴0<
,∴0<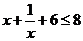 ,∴
,∴ 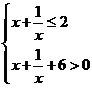

∴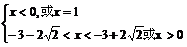

解得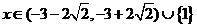

反思:在数的比较大小过程中,要遵循这样的规律,异中求同即先将这些数的部分因式化成相同的部分,再去比较它们剩余部分,就会很轻易啦.一般在数的比较大小中有如下几种方法:(1)作差比较法和作商比较法,前者和零比较,后者和1比较大小;(2)找中间量,往往是1,在这些数中,有的比1大,有的比1小;,(3)计算所有数的值;(4)选用数形结合的方法,画出相应的图形;(5)利用函数的单调性等等.
3.集合的思想和方法在解不等式问题中有广泛的应用,其难点是区分何时取交集,何时取并集.解不等式的另一个难点是含字母系数的不等式求解-注意分类.
2.不等式组的解集是本组各不等式解集的交集,所以在解不等式组时,先要解出本组内各不等式的解集,然后取其交集,在取交集时,一定要利用数轴,将本组内各不等式的解集在同一数轴上表示出来,注意同一不等式解的示意线要一样高,不要将一个不等式解集的两个或几个区间误看成是两个或几个不等式的解集.
1.不等式解法的基本思路
解不等式的过程,实质上是同解不等式逐步代换化简原不等式的过程,因而保持同解变形就成为解不等式应遵循的主要原则,实际上高中阶段所解的不等式最后都要转化为一元一次不等式或一元二次不等式,所以等价转化是解不等式的主要思路.代数化、有理化、整式化、低次化是解初等不等式的基本思路.为此,一要能熟练准确地解一元一次不等式和一元二次不等式,二要保证每步转化都要是等价变形.
4.分式不等式:先整理成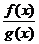 >0或
>0或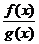 ≥0的形式,转化为整式不等式求解,即:
≥0的形式,转化为整式不等式求解,即:
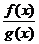 >0
>0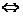 f(x)·g(x)>0
f(x)·g(x)>0
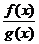 ≥0
≥0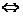
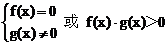

然后用“根轴法”或化为不等式组求解.
3.简单的一元高次不等式:可用区间法(或称根轴法)求解,其步骤是:
①将f(x)的最高次项的系数化为正数;
②将f(x)分解为若干个一次因式的积;
③将每一个一次因式的根标在数轴上,从右上方依次通过每一点画曲线;
④根据曲线显示出的f(x)值的符号变化规律,写出不等式的解集.
2. 一元二次不等式:(如下表)其中a>0,x1,x2是一元二次方程ax2+bx+c=0的两实根,且x1<x2
类型 解集 |
ax2+bx+c>0 |
ax2+bx+c≥0 |
ax2+bx+c<0 |
ax2+bx+c≤0 |
|
Δ>0 |
{x|x<x1或x>x2} |
{x|x≤x1或x≥x2} |
{x|x1<x<x2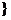 |
{x|x1≤x≤x2} |
|
Δ=0 |
{x|x≠-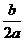 ,x ,x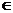 R} R} |
R |
Ф |
{x|x=-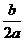 } } |
|
Δ<0 |
R |
R |
Φ |
Φ |
1. 一元一次不等式ax>b
(1)当a>0时,解为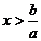 ;
; 
(2)当a<0时,解为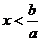 ;
;
(3)当a=0,b≥0时无解;当a=0,b<0时,解为R.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com