
2.已知A是曲线ρ=3cosθ上任意一点,求点A到直线ρcosθ=1距离的最大值和最小值
1.(本小题满分10分)
设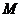 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到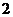 倍,纵坐标伸长到
倍,纵坐标伸长到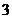 倍的伸压变换.
倍的伸压变换.
(Ⅰ)求矩阵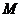 的特征值及相应的特征向量;
的特征值及相应的特征向量;
(Ⅱ)求逆矩阵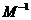 以及椭圆
以及椭圆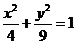 在
在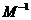 的作用下的新曲线的方程.
的作用下的新曲线的方程.
20.(本题满分16分)
已知函数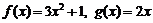 ,数列
,数列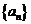 满足对于一切
满足对于一切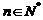 有
有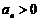 ,且
,且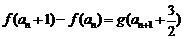 .数列
.数列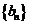 满足
满足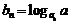 ,设
,设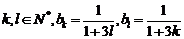 .
.
(Ⅰ)求证:数列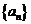 为等比数列,并指出公比;
为等比数列,并指出公比;
(Ⅱ)若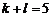 ,求数列
,求数列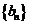 的通项公式;
的通项公式;
(Ⅲ)若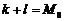 (
(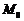 为常数),求数列
为常数),求数列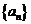 从第几项起,后面的项都满足
从第几项起,后面的项都满足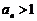 .
.
附加题
19. (本题满分16分)
已知函数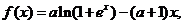 (其中
(其中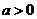 ) ,
) ,
点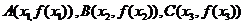 从左到右依次是函数
从左到右依次是函数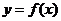 图象上三点,且
图象上三点,且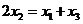 .
.
(Ⅰ) 证明: 函数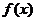 在
在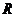 上是减函数;
上是减函数;
(Ⅱ)求证:⊿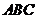 是钝角三角形;
是钝角三角形;
(Ⅲ) 试问,⊿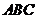 能否是等腰三角形?若能,求⊿
能否是等腰三角形?若能,求⊿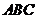 面积的最大值;若不能,请说明理由.
面积的最大值;若不能,请说明理由.
18.(本题满分16分)有如下结论:“圆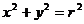 上一点
上一点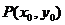 处的切线方程为
处的切线方程为
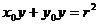 ”,类比也有结论:“椭圆
”,类比也有结论:“椭圆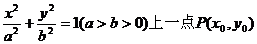 处的切
处的切
线方程为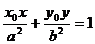 ”,过椭圆C:
”,过椭圆C: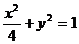 的右准线l上任意一点M引椭圆C的
的右准线l上任意一点M引椭圆C的
两条切线,切点为 A、B.
(1)求证:直线AB恒过一定点;(2)当点M在的纵坐标为1时,求△ABM的面积
17.(本题满分14分) 某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价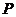 (元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表:
(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表:
|
时间(将第x天记为x)x |
1 |
10 |
11 |
18 |
|
单价(元/件)P |
9 |
0 |
1 |
8 |
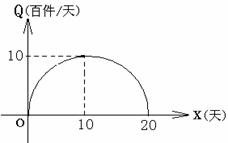
而这20天相应的销售量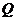 (百件/天)与
(百件/天)与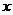 对应的点
对应的点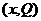 在如图所示的半圆上.
在如图所示的半圆上.
(Ⅰ)写出每天销售收入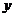 (元)与时间
(元)与时间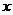 (天)的函数关系式
(天)的函数关系式 ;
;
(Ⅱ)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价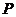 定为多少元为好?(结果精确到1元)
定为多少元为好?(结果精确到1元)
16. (本题满分14分)
(本题满分14分)
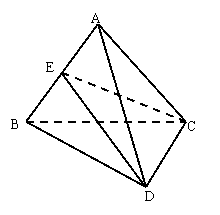
如图,已知空间四边形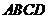 中,
中,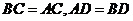 ,
,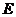 是
是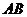 的中点.
的中点.
求证:(1)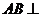 平面CDE;
平面CDE;
(2)平面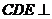 平面
平面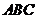 .
.
(3)若G为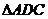 的重心,试在线段AE上确定一点F,使得GF
的重心,试在线段AE上确定一点F,使得GF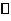 平面CDE.
平面CDE.
15. (本题满分14分)
已知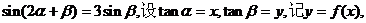
(1)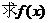 的解析表达式;
的解析表达式;
(2)若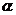 角是一个三角形的最小内角,试求函数
角是一个三角形的最小内角,试求函数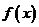 的值域.
的值域.
14.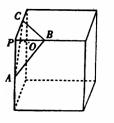 若RtΔABC中两直角边为a、b,斜边c上的高为h,则
若RtΔABC中两直角边为a、b,斜边c上的高为h,则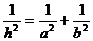 ,如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记M=
,如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记M=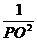 ,N=
,N=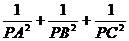 ,那么M、N的大小关系是▲ .
,那么M、N的大小关系是▲ .
13.已知函数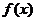 是定义在R上的奇函数,
是定义在R上的奇函数,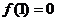 ,
,
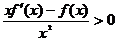
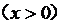 ,则不等式
,则不等式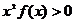 的解集是▲ .
的解集是▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com