
2. 函数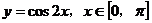 的增区间为 ▲ .
的增区间为 ▲ .
1.已知数集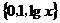 中有三个元素,那么x的取值范围为 ▲ .
中有三个元素,那么x的取值范围为 ▲ .
6. 动点P在x轴与直线l:y=3之间的区域(含边界)上运动,且点P到点F(0,1)和直线l的距离之和为4.
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)过点Q(0,-1)作曲线C的切线,求所作的切线与曲线C所围成的区域的面积.
解:(Ⅰ)设P(x,y),根据题意,得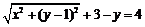 .……………………………3分
.……………………………3分
化简,得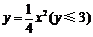 .…………………………………………………………………4分
.…………………………………………………………………4分
(Ⅱ)设过Q的直线方程为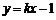 ,代入抛物线方程,整理,得
,代入抛物线方程,整理,得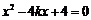 .
.
∴△=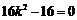 .解得
.解得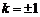 .………………………………………………………6分
.………………………………………………………6分
所求切线方程为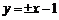 (也可以用导数求得切线方程),
(也可以用导数求得切线方程),
此时切点的坐标为(2,1),(-2,1),且切点在曲线C上. ………………………8分
由对称性知所求的区域的面积为
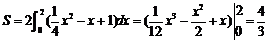 .…………………………………………10分
.…………………………………………10分
说明:抛物线在附加题中的要求提高了,定积分要求不高.
附加题部分说明:
本次附加题考查内容尽量回避一模所考内容,没有考查概率分布和空间向量解立体几何问题.这两部分内容很重要,希望在后期的复习中不可忽视.
5.已知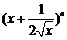 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(Ⅰ)求n的值;
(Ⅱ)求展开式中系数最大的项.
解:(Ⅰ)由题设,得 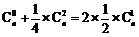 , ………………………………………………3分
, ………………………………………………3分
即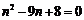 ,解得n=8,n=1(舍去).……………………………………………4分
,解得n=8,n=1(舍去).……………………………………………4分
(Ⅱ)设第r+1的系数最大,则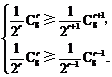 ……………………………………………6分
……………………………………………6分
即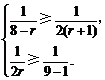 解得r=2或r=3. ………………………………………………8分
解得r=2或r=3. ………………………………………………8分
所以系数最大的项为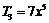 ,
,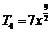 .………………………………………………10分
.………………………………………………10分
说明:掌握二项式定理,展开式的通项及其常见的应用.
4. 选修4-5:不等式选讲
已知x,y,z均为正数.求证: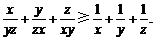
证明:因为x,y,z无为正数.所以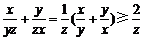 , ………………………………4分
, ………………………………4分
同理可得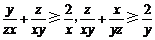 ,………………………………………………………7分
,………………………………………………………7分
当且仅当x=y=z时,以上三式等号都成立.
将上述三个不等式两边分别相加,并除以2,得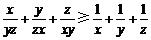 .…………10分
.…………10分
3. 选修4-4:坐标系与参数方程
过点P(-3,0)且倾斜角为30°的直线和曲线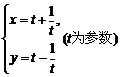 相交于A、B两点.求线段AB的长.
相交于A、B两点.求线段AB的长.
解:直线的参数方程为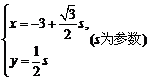 ,………………………………………………3分
,………………………………………………3分
曲线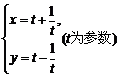 可以化为
可以化为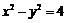 .……………………………………………5分
.……………………………………………5分
将直线的参数方程代入上式,得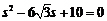 .
.
设A、B对应的参数分别为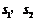 ,∴
,∴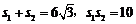 .…………………………8分
.…………………………8分
AB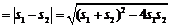 =
=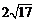 .…………………………………………………10分
.…………………………………………………10分
说明:掌握直线,圆,圆锥曲线的参数方程及简单的应用.
2. 选修4-2:矩阵与变换
 如图所示, 四边形ABCD和四边形
如图所示, 四边形ABCD和四边形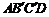 分别是矩形和平行四边
分别是矩形和平行四边
形,其中点的坐标分别为A(-1,2),B(3,2),C(3,-2),
D(-1,-2),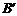 (3,7),
(3,7),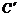 (3,3).求将四边形ABCD变成
(3,3).求将四边形ABCD变成
四边形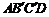 的变换矩阵M.
的变换矩阵M.
解:该变换为切变变换,设矩阵M为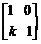 ,…………………3分
,…………………3分
则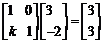 .………………………………………………6分
.………………………………………………6分
∴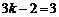 ,解得
,解得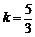 .…………………………………………………………………9分
.…………………………………………………………………9分
所以,M为 .………………………………………………………………………10分
.………………………………………………………………………10分
说明:掌握几种常见的平面变换.
1. 选修4-1:几何证明选讲
 如图,四边形ABCD内接于
如图,四边形ABCD内接于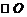 ,
,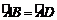 ,过A点的切线交CB
,过A点的切线交CB
的延长线于E点.
求证: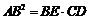 .
.
证明:连结AC.…………………………………………………1分
因为EA切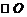 于A, 所以∠EAB=∠ACB.…………3分
于A, 所以∠EAB=∠ACB.…………3分
 因为
因为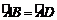 ,所以∠ACD=∠ACB,AB=AD.
,所以∠ACD=∠ACB,AB=AD.
于是∠EAB=∠ACD.…………………………………5分
又四边形ABCD内接于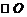 ,所以∠ABE=∠D.
,所以∠ABE=∠D.
所以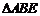 ∽
∽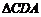 .
.
于是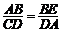 ,即
,即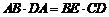 .………………9分
.………………9分
所以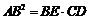 .…………………………………10分
.…………………………………10分
20.(本小题满分16分)
已知数列 中,
中,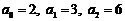 ,且对
,且对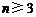 时,有
时,有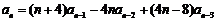 .
.
(Ⅰ)设数列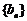 满足
满足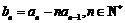 ,证明数列
,证明数列 为等比数列,并求数列
为等比数列,并求数列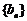 的通项公式;
的通项公式;
(Ⅱ)记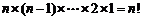 ,求数列
,求数列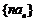 的前n项和Sn.
的前n项和Sn.
(Ⅰ) 证明:由条件,得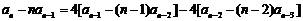 ,
,
则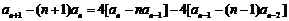 .……………………………………2分
.……………………………………2分
即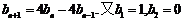 ,所以
,所以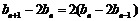 ,
,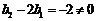 .
.
所以 是首项为
是首项为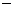 2,公比为2的等比数列. …………………………………4分
2,公比为2的等比数列. …………………………………4分
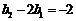 ,所以
,所以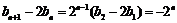 .
.
两边同除以 ,可得
,可得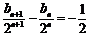 .…………………………………………………6分
.…………………………………………………6分
于是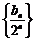 为以
为以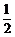 首项,-
首项,-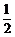 为公差的等差数列.
为公差的等差数列.
所以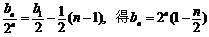 .………………………………………………8分
.………………………………………………8分
(Ⅱ)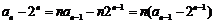 ,令
,令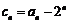 ,则
,则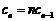 .
.
而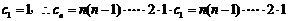 .
.
∴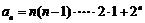 . ……………………………………………………………12分
. ……………………………………………………………12分
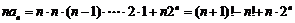 ,
,
∴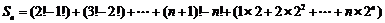 .………………14分
.………………14分
令Tn=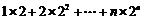 , ①
, ①
则2Tn=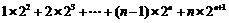 . ②
. ②
①-②,得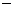 Tn=
Tn=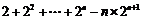 ,Tn=
,Tn=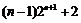 .
.
∴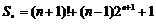 .……………………………………………………………16分
.……………………………………………………………16分
评讲建议:
此题主要考查数列的概念、等差数列、等比数列、数列的递推公式、数列的通项求法、数列前n项和的求法,作新数列法,错项相消法,裂项法等知识与方法,同时考查学生的分析问题与解决问题的能力,逻辑推理能力及运算能力.讲评时着重在正确审题,怎样将复杂的问题化成简单的问题,本题主要将一个综合的问题分解成几个常见的简单问题.事实上本题包含了好几个常见的数列题.本题还有一些另外的解法,如第一问的证明还可以直接代.
B.附加题部分
19.(本小题满分16分)
已知函数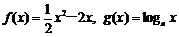 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果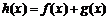 是增函数,且
是增函数,且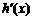 存在零点(
存在零点(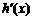 为
为 的导函数).
的导函数).
(Ⅰ)求a的值;
(Ⅱ)设A(x1,y1)、B(x2,y2)(x1<x2)是函数y=g(x)的图象上两点,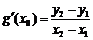 (
(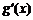 为
为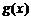 的导函数),证明:
的导函数),证明: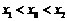 .
.
解:(Ⅰ)因为
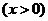 ,
,
所以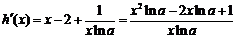 . …………………………………………3分
. …………………………………………3分
因为h(x)在区间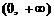 上是增函数,
上是增函数,
所以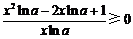 在区间
在区间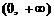 上恒成立.
上恒成立.
若0<a<1,则lna<0,于是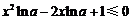 恒成立.
恒成立.
又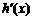 存在正零点,故△=(-2lna)2-4lna=0,lna=0,或lna=1与lna<0矛盾.
存在正零点,故△=(-2lna)2-4lna=0,lna=0,或lna=1与lna<0矛盾.
所以a>1.
由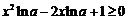 恒成立,又
恒成立,又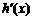 存在正零点,故△=(-2lna)2-4lna=0,
存在正零点,故△=(-2lna)2-4lna=0,
所以lna=1,即a=e. ……………………………………………………………………7分
(Ⅱ)由(Ⅰ),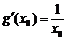 ,于是
,于是 ,
,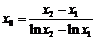 .…………………………9分
.…………………………9分
以下证明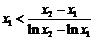 . (※)
. (※)
(※)等价于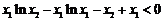 . ……………………………………………11分
. ……………………………………………11分
令r(x)=xlnx2-xlnx-x2+x,…………………………………………………………13分
r ′(x)=lnx2-lnx,在(0,x2]上,r′(x)>0,所以r(x)在(0,x2]上为增函数.
当x1<x2时,r(x1)< r(x2)=0,即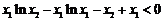 ,
,
从而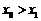 得到证明.……………………………………………………………………15分
得到证明.……………………………………………………………………15分
对于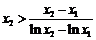 同理可证……………………………………………………………16分
同理可证……………………………………………………………16分
所以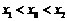 .
.
评讲建议:
此题主要考查函数、导数、对数函数、二次函数等知识.评讲时注意着重导数在研究函数中的应用.本题的第一小题是常规题比较容易,第二小题是以数学分析中的中值定理为背景,作辅助函数,利用导数来研究函数的性质,是近几年高考的热点.第二小题还可以这样证明:
要证明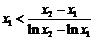 ,只要证明
,只要证明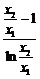 >1,令
>1,令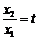 ,作函数h(x)=t-1-lnt,下略.
,作函数h(x)=t-1-lnt,下略.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com