
2.(2009全国卷Ⅰ理)本小题满分12分。(注意:在试题卷上作答无效)
设函数 在两个极值点
在两个极值点 ,且
,且
(I)求 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点 的区域;
的区域;
(II)证明:
 分析(I)这一问主要考查了二次函数根的分布及线性规划作可行域的能力。
分析(I)这一问主要考查了二次函数根的分布及线性规划作可行域的能力。
大部分考生有思路并能够得分。 由题意知方程
由题意知方程 有两个根
有两个根


 则有
则有

 故有
故有
 右图中阴影部分即是满足这些条件的点
右图中阴影部分即是满足这些条件的点 的区域。
的区域。
(II)这一问考生不易得分,有一定的区分度。主要原因是含字母较多,不易找到突破口。此题主要利用消元的手段,消去目标 中的
中的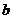 ,(如果消
,(如果消 会较繁琐)再利用
会较繁琐)再利用 的范围,并借助(I)中的约束条件得
的范围,并借助(I)中的约束条件得 进而求解,有较强的技巧性。
进而求解,有较强的技巧性。
解: 由题意有 ............①
............①
又 .....................②
.....................②
消去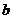 可得
可得 .
.
又 ,且
,且

1.(2009年广东卷文)(本小题满分14分)
已知二次函数 的导函数的图像与直线
的导函数的图像与直线 平行,且
平行,且 在
在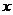 =-1处取得最小值m-1(m
=-1处取得最小值m-1(m ).设函数
).设函数
(1)若曲线 上的点P到点Q(0,2)的距离的最小值为
上的点P到点Q(0,2)的距离的最小值为 ,求m的值
,求m的值
(2)  如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
[解析](1)设 ,则
,则 ;
;
又 的图像与直线
的图像与直线 平行
平行 
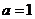
又 在
在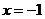 取极小值,
取极小值,  ,
, 
 ,
,  ;
;
 , 设
, 设
则


 ;21世纪教育网
;21世纪教育网
(2)由 ,
,
得 

当 时,方程
时,方程 有一解
有一解 ,函数
,函数 有一零点
有一零点 ;
;
当 时,方程
时,方程 有二解
有二解 ,若
,若 ,
, ,
,
函数 有两个零点
有两个零点 ;若
;若 ,
,
 ,函数
,函数 有两个零点
有两个零点 ;
;
当 时,方程
时,方程 有一解
有一解 ,
,  ,
函数
,
函数 有一零点
有一零点 21世纪教育网
21世纪教育网
19.(2009重庆卷文)记 的反函数为
的反函数为 ,则方程
,则方程 的解
的解 .
.
[答案]2
解法1由 ,得
,得 ,即
,即 ,于是由
,于是由 ,解得
,解得
解法2因为 ,所以
,所以
18.(2009宁夏海南卷文)曲线 在点(0,1)处的切线方程为
。
在点(0,1)处的切线方程为
。
[答案]
[解析] ,斜率k=
,斜率k= =3,所以,y-1=3x,即
=3,所以,y-1=3x,即
16.(2009陕西卷理)设曲线 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为 ,令
,令 ,则
,则 的值为
.
的值为
.
答案:-2

15.(2009福建卷理)若曲线 存在垂直于
存在垂直于 轴的切线,则实数
轴的切线,则实数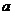 取值范围是_____________.
取值范围是_____________.
[答案]:
解析:由题意可知 ,又因为存在垂直于
,又因为存在垂直于 轴的切线,
轴的切线,
所以 。
。
13.(2009山东卷文)若函数f(x)=a -x-a(a>0且a
-x-a(a>0且a 1)有两个零点,则实数a的取值范围是 .
1)有两个零点,则实数a的取值范围是 .
[解析]: 设函数 且
且 和函数
和函数 ,则函数f(x)=a
,则函数f(x)=a -x-a(a>0且a
-x-a(a>0且a 1)有两个零点, 就是函数
1)有两个零点, 就是函数 且
且 与函数
与函数 有两个交点,由图象可知当
有两个交点,由图象可知当 时两函数只有一个交点,不符合,当
时两函数只有一个交点,不符合,当 时,因为函数
时,因为函数 的图象过点(0,1),而直线
的图象过点(0,1),而直线 所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是
所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是 .
.
答案: 
[命题立意]:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数的不同取值范围而分别画出函数的图象进行解答.
12.(2009山东卷理)已知定义在R上的奇函数 ,满足
,满足 ,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间
,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间 上有四个不同的根
上有四个不同的根 ,则
,则
[解析]:因为定义在R上的奇函数,满足 ,所以
,所以 ,所以, 由
,所以, 由 为奇函数,所以函数图象关于直线
为奇函数,所以函数图象关于直线 对称且
对称且 ,由
,由 知
知 ,所以函数是以8为周期的周期函数,又因为
,所以函数是以8为周期的周期函数,又因为 在区间[0,2]上是增函数,所以
在区间[0,2]上是增函数,所以 在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间
在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间 上有四个不同的根
上有四个不同的根 ,不妨设
,不妨设 由对称性知
由对称性知
 所以
所以
 答案:-8
答案:-8
[命题立意]:本题综合考查了函数的奇偶性,单调性,
对称性,周期性,以及由函数图象解答方程问题,
运用数形结合的思想和函数与方程的思想解答问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com