
2.难点是学生有初中的知识,往往误认为压力N的大小总是跟滑动物体所受的重力相
等,因此必须指出只有当两物体的接触面垂直,物体在水平拉力作用下,沿水平面滑动时,压力N的大小才跟物体所受的重力相等。
1.本节课的内容分滑动摩擦力和静摩擦力两部分。重点是摩擦力产生的条件、特性和规律,通过演示实验得出关系f=μN。
3.情感态度价值观:
在分析物体所受摩擦力时,突出主要矛盾,忽略次要因素及无关因素,总结出摩擦力产生的条件和规律。
l.知识与技能:
(1)知道摩擦力产生的条件。
(2)能在简单问题中,根据物体的运动状态,判断静摩擦力的有无、大小和方向;知道存在着最大静摩擦力。
(3)掌握动磨擦因数,会在具体问题中计算滑动磨擦力,掌握判定摩擦力方向的方法。
(4)知道影响到摩擦因数的因素。
2.过程与方法:
通过观察演示实验,概括出摩擦力产生的条件及摩擦力的特点,培养学生的观察、概括能力。通过静摩擦力与滑动摩擦力的区别对比,培养学生分析综合能力。
38.(2009重庆卷文)(本小题满分12分,(Ⅰ)问7分,(Ⅱ)问5分)
已知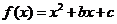 为偶函数,曲线
为偶函数,曲线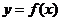 过点
过点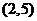 ,
,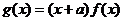 .
.
(Ⅰ)求曲线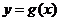 有斜率为0的切线,求实数
有斜率为0的切线,求实数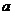 的取值范围;
的取值范围;
(Ⅱ)若当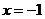 时函数
时函数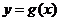 取得极值,确定
取得极值,确定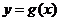 的单调区间.
的单调区间.
解: (Ⅰ)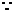
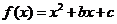 为偶函数,故
为偶函数,故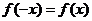 即有
即有
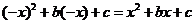 解得
解得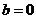
又曲线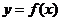 过点
过点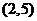 ,得
,得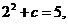 有
有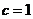
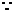
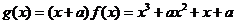 从而
从而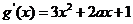 ,
,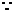 曲线
曲线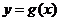 有斜率为0的切线,故有
有斜率为0的切线,故有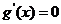 有实数解.即
有实数解.即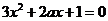 有实数解.此时有
有实数解.此时有 解得
解得
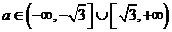 所以实数
所以实数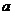 的取值范围:
的取值范围: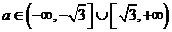
(Ⅱ)因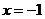 时函数
时函数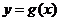 取得极值,故有
取得极值,故有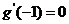 即
即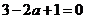 ,解得
,解得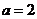
又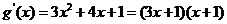 令
令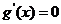 ,得
,得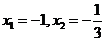
当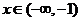 时,
时, 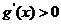 ,故
,故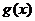 在
在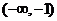 上为增函数
上为增函数
当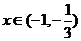 时,
时, 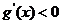 ,故
,故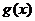 在
在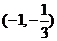 上为减函数
上为减函数
当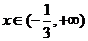 时,
时, 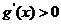 ,故
,故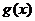 在
在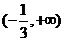 上为增函数21世纪教育网
上为增函数21世纪教育网 

37.(2009重庆卷理)(本小题满分13分,(Ⅰ)问5分,(Ⅱ)问8分)
设函数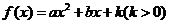 在
在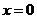 处取得极值,且曲线
处取得极值,且曲线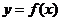 在点
在点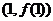 处的切线垂直于直线
处的切线垂直于直线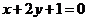 .
.
(Ⅰ)求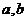 的值;
的值;
(Ⅱ)若函数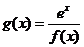 ,讨论
,讨论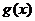 的单调性.
的单调性.
解(Ⅰ)因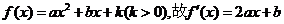
又 在x=0处取得极限值,故
在x=0处取得极限值,故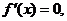 从而
从而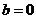 21世纪教育网
21世纪教育网 

由曲线y= 在(1,f(1))处的切线与直线
在(1,f(1))处的切线与直线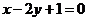 相互垂直可知
相互垂直可知
该切线斜率为2,即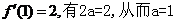
(Ⅱ)由(Ⅰ)知,
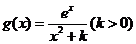
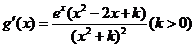
令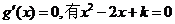
(1)当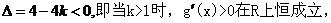
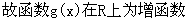
(2)当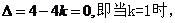
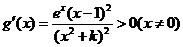
K=1时,g(x)在R上为增函数
(3)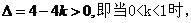 方程
方程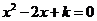 有两个不相等实根
有两个不相等实根
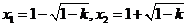 21世纪教育网
21世纪教育网 

当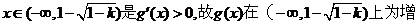 函数
函数
当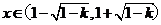 时,
时,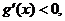 故
故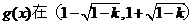 上为减函数
上为减函数
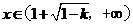 时,
时,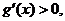 故
故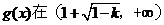 上为增函数
上为增函数
36.(2009上海卷文)(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分 .有时可用函数
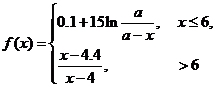
描述学习某学科知识的掌握程度.其中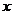 表示某学科知识的学习次数(
表示某学科知识的学习次数(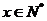 ),
),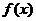 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1)证明:当x 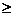 7时,掌握程度的增长量f(x+1)- f(x)总是下降;
7时,掌握程度的增长量f(x+1)- f(x)总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],
(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
证明(1)当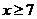 时,
时,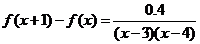
而当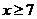 时,函数
时,函数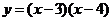 单调递增,且
单调递增,且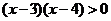
故函数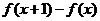 单调递减
单调递减
当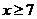 时,掌握程度的增长量
时,掌握程度的增长量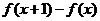 总是下降21世纪教育网
总是下降21世纪教育网 

(2)有题意可知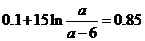
整理得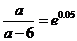
解得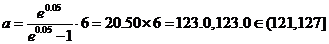 …….13分
…….13分
由此可知,该学科是乙学科……………..14分
35.(2009年上海卷理)(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分。
已知函数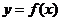 的反函数。定义:若对给定的实数
的反函数。定义:若对给定的实数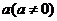 ,函数
,函数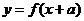 与
与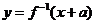 互为反函数,则称
互为反函数,则称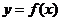 满足“
满足“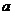 和性质”;若函数
和性质”;若函数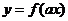 与
与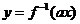 互为反函数,则称
互为反函数,则称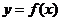 满足“
满足“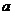 积性质”。
积性质”。
(1)
判断函数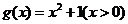 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2) 求所有满足“2和性质”的一次函数;
(3)
设函数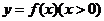 对任何
对任何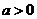 ,满足“
,满足“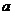 积性质”。求
积性质”。求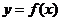 的表达式。
的表达式。
解:(1)函数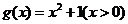 的反函数是
的反函数是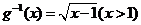
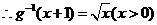
而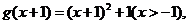 其反函数为
其反函数为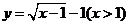
故函数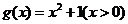 不满足“1和性质”
不满足“1和性质”
(2)设函数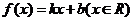 满足“2和性质”,
满足“2和性质”,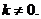
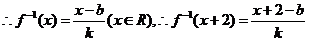 …….6分
…….6分
而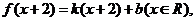 得反函数
得反函数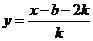 ………….8分
………….8分
由“2和性质”定义可知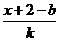 =
=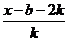 对
对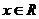 恒成立
恒成立
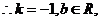 即所求一次函数为
即所求一次函数为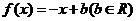 ………..10分
………..10分
(3)设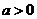 ,
,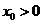 ,且点
,且点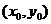 在
在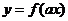 图像上,则
图像上,则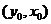 在函数
在函数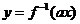 图象上,
图象上,
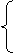 故
故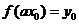 ,可得
,可得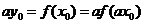 ,
......12分
,
......12分
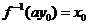 ,
,
令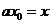 ,则
,则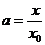 。
。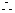
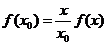 ,即
,即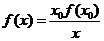 。 ......14分
。 ......14分
综上所述,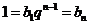
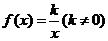 ,此时
,此时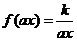 ,其反函数就是
,其反函数就是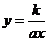 ,
,
而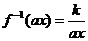 ,故
,故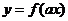 与
与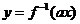 互为反函数 。
......16分
互为反函数 。
......16分
34.(2009年上海卷理)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分。
有时可用函数
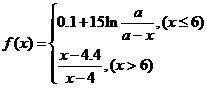
描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(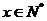 ),
), 表示对该学科知识的掌握程度,正实数a与学科知识有关。
表示对该学科知识的掌握程度,正实数a与学科知识有关。
(1)
证明:当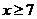 时,掌握程度的增加量
时,掌握程度的增加量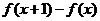 总是下降;
总是下降;
(2)
根据经验,学科甲、乙、丙对应的a的取值区间分别为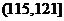 ,
,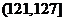 ,
,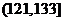 。当学习某学科知识6次时,掌握程度是85%,请确定相应的学科。
。当学习某学科知识6次时,掌握程度是85%,请确定相应的学科。
证明(1)当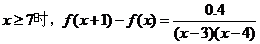
而当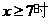 ,函数
,函数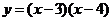 单调递增,且
单调递增,且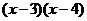 >0……..3分
>0……..3分
故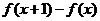 单调递减
单调递减
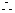 当
当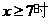 ,掌握程度的增长量
,掌握程度的增长量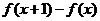 总是下降……………..6分
总是下降……………..6分
(2)由题意可知0.1+15ln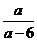 =0.85……………….9分
=0.85……………….9分
整理得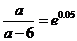
解得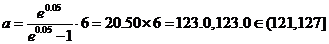 …….13分
…….13分
由此可知,该学科是乙学科……………..14分
33.(2009福建卷文)(本小题满分12分)
已知函数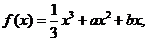 且
且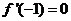
(I)试用含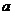 的代数式表示
的代数式表示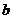 ;
;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)令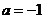 ,设函数
,设函数 在
在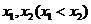 处取得极值,记点
处取得极值,记点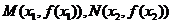 ,证明:线段
,证明:线段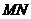 与曲线
与曲线 存在异于
存在异于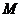 、
、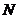 的公共点;
的公共点;
解法一:
(I)依题意,得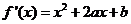
由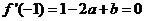 得
得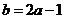
(Ⅱ)由(I)得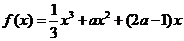 (
(
故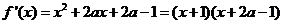
令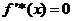 ,则
,则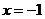 或
或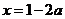
①当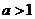 时,
时,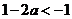
当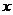 变化时,
变化时,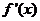 与
与 的变化情况如下表:
的变化情况如下表:
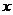 |
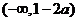 |
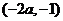 |
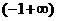 |
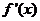 |
+ |
- |
+ |
 |
单调递增 |
单调递减 |
单调递增 |
由此得,函数 的单调增区间为
的单调增区间为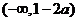 和
和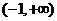 ,单调减区间为
,单调减区间为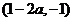
②由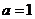 时,
时,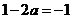 ,此时,
,此时,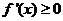 恒成立,且仅在
恒成立,且仅在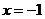 处
处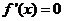 ,故函数
,故函数 的单调区间为R
的单调区间为R
③当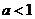 时,
时,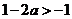 ,同理可得函数
,同理可得函数 的单调增区间为
的单调增区间为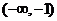 和
和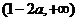 ,单调减区间为
,单调减区间为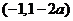
综上:21世纪教育网 

当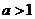 时,函数
时,函数 的单调增区间为
的单调增区间为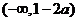 和
和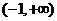 ,单调减区间为
,单调减区间为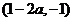 ;
;
当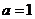 时,函数
时,函数 的单调增区间为R;
的单调增区间为R;
当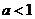 时,函数
时,函数 的单调增区间为
的单调增区间为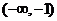 和
和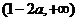 ,单调减区间为
,单调减区间为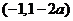
(Ⅲ)当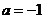 时,得
时,得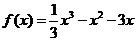
由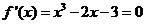 ,得
,得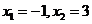
由(Ⅱ)得 的单调增区间为
的单调增区间为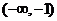 和
和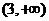 ,单调减区间为
,单调减区间为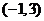
所以函数 在
在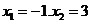 处取得极值。
处取得极值。
故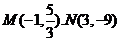
所以直线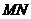 的方程为
的方程为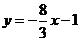
由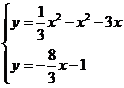 得
得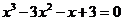
令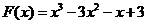
易得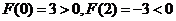 ,而
,而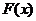 的图像在
的图像在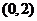 内是一条连续不断的曲线,
内是一条连续不断的曲线,
故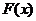 在
在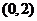 内存在零点
内存在零点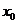 ,这表明线段
,这表明线段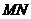 与曲线
与曲线 有异于
有异于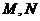 的公共点
的公共点
解法二:
(I)同解法一
(Ⅱ)同解法一。
(Ⅲ)当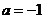 时,得
时,得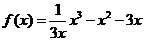 ,由
,由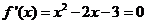 ,得
,得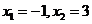
由(Ⅱ)得 的单调增区间为
的单调增区间为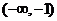 和
和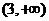 ,单调减区间为
,单调减区间为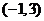 ,所以函数
,所以函数 在
在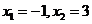 处取得极值,21世纪教育网
处取得极值,21世纪教育网 

故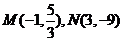
所以直线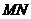 的方程为
的方程为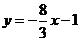
由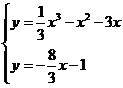 得
得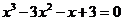
解得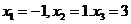
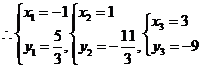
所以线段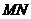 与曲线
与曲线 有异于
有异于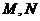 的公共点
的公共点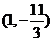
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com