由此求得圆心距为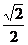,选D.

评述:本题考查对极坐标的理解,理解深刻者可在极坐标系上画出简图直接求解,

一般理解者,化极坐标方程为直角坐标方程也能顺利得到正确答案.

解法二:将极坐标方程化成直角坐标方程得(x-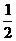)²+y²=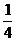与x²+(y-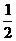)²=,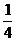

解法一:两圆的圆心坐标分别为(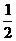,0)与(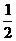,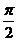),由此求得圆心距为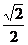,选D.

    (A)   2           (B) 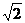           (C)  1          (D)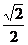   

例13(1992年全国、1996年上海)极坐标方程分别是=cos和=sin的两个圆的圆心距是

点(2,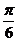)在直角坐标系中为(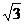,1),故点(2,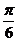) 到直线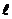的距离为2.

评注：本题主要考查极坐标系与直角坐标系之间的互化.

解: 将直线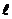的极坐标方程ρsinθ=3化为直角坐标系方程得:y=3,

例12(2007广东文)在极坐标系中，直线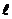的方程为ρsinθ=3，则点(2,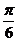)到直线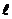的距离为___________.

类题：(2002上海)若A、B两点的极坐标为A(4,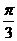),B(6,0),则AB中点的极坐标是_________.(极角用反三角函数值表示).           答案.()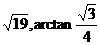

六、求距离

  所以所求圆心坐标为(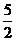,arcsin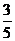),故选A.