四棱锥P―ABCD的体积V_P―ABCD=

的平面角，由已知条件可知∠PEO=60°，PE=6，所以PO=3，

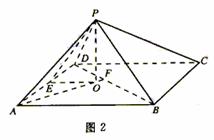变式：如图，四棱锥P―ABCD中，底面ABCD 为矩形，AB=8，AD=4，侧面PAD为等边三角形，并且与底面所成二面角为60°.

（Ⅰ）求四棱锥P―ABCD的体积；

（Ⅱ）证明PA⊥BD.

 解析：（Ⅰ）如图，取AD的中点E，

连结PE，则PE⊥AD.

作PO⊥平面在ABCD，垂足为O，连结OE.

根据三垂线定理的逆定理得OE⊥AD，

所以∠PEO为侧面PAD与底面所成的二面角

∴AE=时，二面角D₁―EC―D的大小为.

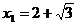∴（不合，舍去）， .

∴依题意

由  令b=1,  ∴c=2, a=2－x，

∴

（3）设平面D₁EC的法向量，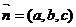

从而，所以点E到平面AD₁C的距离为