解  ∵  k_AB?k_OM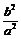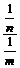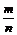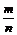＝－＝－＝－,∴ ＝－k_AB?k_OM＝1?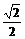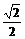＝，故选Ａ．

分析:命题：“若斜率为k(k≠0)的直线与椭圆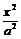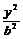＋＝1（或双曲线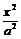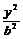－＝1）相交于A、B的中点，则k?k_OM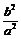＝－(或k?k_OM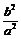＝)，”（证明留给读者）在处理有关圆锥曲线的中点弦问题中有着广泛的应用．运用这一结论，不难得到：

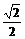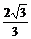Ａ.              Ｂ.              Ｃ.1            Ｄ.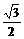

例3、  椭圆mx²＋ny²＝1与直线x＋y＝1交于A、B两点，过AB中点M与原点的直线斜率为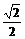，则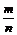的值为（     ）

又∵ |PF₁|²＋|PF₂|²＝(2c)²＝20.∴ 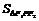 ＝1，选Ａ．

∵ ∠F₁PF₂＝90^o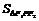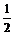，∴ ＝|PF₁|?|PF₂|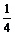＝(|PF₁|²＋|PF₂|²－16).

Ａ.1                 Ｂ.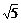/2               Ｃ.2               Ｄ.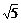

解  ∵ |PF₁|－|PF₂|＝±2a＝±4，∴ |PF₁|²＋|PF₂|²－2|PF₁|?|PF₂|＝16，

例2、设F₁、F₂为双曲线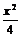－y²＝1的两个焦点，点P在双曲线上满足∠F₁PF₂＝90^o，则△F₁PF₂的面积是（    ）

解 :本题的关键是确定已知直线与圆的相对位置,这就需对圆心到直线的距离作定量分析．将圆的方程化为(x＋1)²＋(y＋2)²＝(2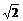)²,∴  r＝2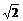.∵  圆心(－1，－2)到直线x＋y＋1＝0的距离d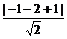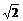＝＝,恰为半径的一半．故选Ｃ．

例1、 圆x²＋2x＋y²＋4y－3＝0上到直线x＋y＋1＝0的距离为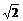的点共有（    ）

Ａ.1个               Ｂ.2个              Ｃ.3个              Ｄ.4个