
而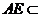 平面
平面 ,
, .
.
 ,
, 平面
平面 .
.
因 底面
底面 ,
, 平面
平面 ,故
,故 .
.
(Ⅰ)证明:在四棱锥 中,
中,
(Ⅲ)求二面角 的大小.
的大小.
(Ⅱ)证明 平面
平面 ;
;
 (Ⅰ)证明
(Ⅰ)证明 ;
;
【范例1】如图,在四棱锥 中,
中, 底面
底面 ,
, ,
, ,
, 是
是 的中点.
的中点.
 ;
;
★★★高考将考什么
得 所以Rt△AEO∽Rt△BAD.得∠EAO=∠ABD.
所以Rt△AEO∽Rt△BAD.得∠EAO=∠ABD.
所以∠EAO+∠ADF=90° 所以 AF⊥BD.
因为 直线AF为直线PA在平面ABCD 内的身影,所以PA⊥BD.
【点晴】本小题主要考查棱锥的体积、二面角、异面直线所成的角等知识和空间想象能力、分析问题能力,解题的关键是二面角的使用。使用空间向量能降低对空间想象能力的要求,但坐标系的位置不规则,注意点坐标的表示。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com