
注:直接运用半角公式求tg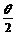 ,将会错选(A).若直接计算,由(
,将会错选(A).若直接计算,由(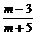 )2+(
)2+(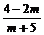 )2=1,可得m=0或m=8,∵
)2=1,可得m=0或m=8,∵ 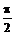 <q <p, ∴ sinq >0,cosq <0,故应舍去m=0,取m=8,得sinq =
<q <p, ∴ sinq >0,cosq <0,故应舍去m=0,取m=8,得sinq =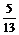 ,cosq =
,cosq =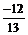 ,再由半角公式求出tg=
,再由半角公式求出tg=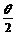 =5,也不如上述解法简捷.
=5,也不如上述解法简捷.
解 因受条件sin2q +cos2q =1的制约,故m为一确定值,于是sinq 、cosq 的值应与m无关,进而推知tg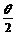 的值与m无关,∵
的值与m无关,∵ 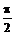 <q <p, ∴
<q <p, ∴ 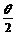 Î(
Î(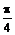 ,
,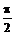 ),∴
tg
),∴
tg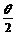 >1,故选(D).
>1,故选(D).
A.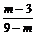 B.|
B.|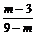 |
C.
|
C.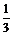 D.5
D.5
例3、已知sinq =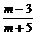 ,cosq =
,cosq =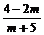 (
(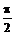 <q <p),则tg
<q <p),则tg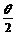 =( ).
=( ).
解 ∵ 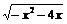 ≥0, ∴ (A)真Þ(B)真Þ(C)真Þ(D)真,
∴ (D)真.
≥0, ∴ (A)真Þ(B)真Þ(C)真Þ(D)真,
∴ (D)真.
A.5
B.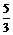 C.-
C.-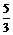 D.-5
D.-5
例1 当xÎ[-4,0]时,a+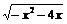 ≤
≤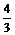 x+1恒成立,则a的一个可能值是( )
x+1恒成立,则a的一个可能值是( )
A.(4.5,3) B.(3,6) C.(9,2) D.(6,4)
解:一一代入检验。代入运算后比较大小。
7、推理分析法
通过对四个选择支之间的逻辑关系的分析,达到否定谬误支,肯定正确支的方法,称之为逻辑分析法,例如:若“(A)真 Þ (B)真”,则(A)必假,否则将与“只有一个选择支正确”的前提相矛盾.
例3.(2004广东)变量x,y满足下列条件: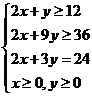
则使得z=3x+2y的值的最小的(x,y)是( B )
例2.已知二次函数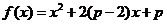 ,若在区间[0,1]内至少存在一个实数c,使
,若在区间[0,1]内至少存在一个实数c,使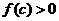 ,则实数p的取值范围是( C )
,则实数p的取值范围是( C )
A.(1,4) B.(1,+∞) C.(0,+∞) D.(0,1)
解:取p=1代入检验。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com