1．默写。(6分)

(1)三山半落青天外，______________________。(《登金障凤凰台》)

   (2)莫道不消魂，帘卷西风，______________________。(《醉花阴》)

   (3) ______________________，拾此充饥肠。(《观刈麦》)

   (4)过尽千帆皆不是，______________________。(《望江南》)

(5)子曰：“由，诲女知之乎! ______________________，是知也。”(《<论语>》十则)

(6) ______________________，不求闻达于诸侯。（《出师表》) 

⑶用配方法将函数的解析式化为的形式；

⑷指出日销售额最大时每台计算机的售价应为多少?

25．（本小题满分12分）

某计算机商店销售计算机，经统计每台售价9000元时，每天销售20台，而降价销售则销量增加，每台每降价300元，日销量增加一台，设日销量增加x台， 日销售额为y元

⑴用含x的代数式分别表示出日销量增加后每天的销量和每台计算机的售价；

⑵写出y与x之间的函数关系式；

⑶当点E、F、M、N不再处于正方形ABCD四条边AB、BC、CD、DA特殊的位置时，猜想线段EF、MN满足什么位置关系时，才会有EF=MN，画出相应的图形，并证明你的猜想。

24．（本小题满分12分）

如图13-1，E、F、M、N是正方形ABCD四条边AB、BC、CD、DA上

可以移动的四个点，每组对边上的两个点，可以连接成一条线段。

⑴如图13-2，如果EF∥BC， MN∥CD，

那么EF      MN（位置），EF      MN（大小）

⑵如图13-3，如果E与A，F与C，M与B，N与D重合，

那么EF      MN（位置），EF      MN（大小）

（1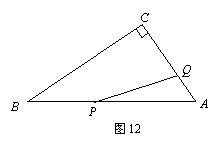）       用含t的代数式表示线段AP，AQ的长；

（2）       当t为何值时△APQ是以PQ为底的等腰三角形？

（3）       当t为何值时PQ∥BC？

23．（本小题满分8分）

   如图12，在Rt△ABC中，∠C=90°，∠A=60°，AB=12cm，若点P从B点出发以2cm/秒的速度向A点运动，点Q从A点出发以1cm/秒的速度向C点运动，设P、Q分别从B、A同时出发，运动时间为t秒。解答下列问题：

观察上面的数表，你发现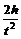的值有什么变化规律吗？ 请你写出用t表示h的表达式．