如图(1)是腰长分别是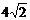和2的两个等腰直角三角形ABC和C^‘D^‘E^‘叠放在一起(C与C^’重合)．

   (1)固定△ABC，将△C^‘D^‘E^‘绕点C顺时针旋转45°得到△CDE，如图(2)，若连结BE、  AD，请你判断BE与AD的大小关系，并证明你的结论；

   (2)延长CE交AB于K点，将图(2)中的△CDE在线段CK上沿着CK方向以每秒1个单位长度的速度平移，如图(3)，将平移后的△CDE设为△PQR，设△PQR移动的时间为x秒，点P运动到K点停止，设△PQR与△AKC重叠的面积为y，求y与x的函数关系式，并写出自变量x的取值范围；

24．(本题满分12分)

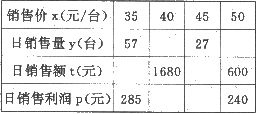
(1)请根据题意和表中已有的数据，在表中空白处填上适当的数；

(2)如图，在平面直角坐标系中，根据(1)中的数据，描出实数对(x，y)的对应点，根据你的猜测写出y与x的一个函数关系式；

    (3)根据(2)中的关系写出p与x的函数关系式，并指出当销售价x为多少元时，才能获得最大的销售利润?

23．(本题满分8分)

某商场经营一批进价为a元／台的小加湿器，经调查得到下面表中的数据：

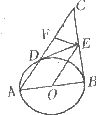已知，以Rt△ABC的直角边AB为直径作圆O，与斜边AC交于点D，过点D作圆O的切线交BC边于点E．

(1)如图，求证EB=EC=ED

(2)若∠DEF=∠C，EF交DC于点F

求证：BC²=4DF?DC

22．(本题满分8分)

21．(本题满分8分)

关于x的方程k²x²+2(k-1)x+1=0。有实数根．

(1)求k的取值范围；   

(2)如果这个方程的两个实数根的倒数和的平方等于8，求k的值．

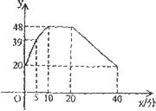    (1)当O≤x≤10时，求注意力的指标y随时间x变化的函数关系式，

    (2)现有一节课需要老师讲24分钟，何老师是否能经过适当的安排，使学生在听课时能够保证注意力的指标数一直不低于36?

20．(本题满分8分)

通过实验研究，专家们发现，初中学生听课的注意力指标是随着老师讲课时间变化而变化的，讲课开始时，学生的兴趣激增，中间有一段时间，学生的兴趣保持平稳的状态，随后开始分散．学生注意力的指标，y 随时间x(分)变化的图象如图所示(y越大注意力越集中)．当0≤x≤10时，图象是抛物线的一部分，当10≤x≤20和20≤x≤40时，图象是线段．

19．(本题满分8分)

为了培养同学们的综合实践能力，某数学老师让大家测量校园内的一棵高大松柏树，要测出它的高度，不能爬到树尖上去，也不能将树砍倒．老师提供的工具有小镜子和测量土地用的圈尺，请你写出两种测量方法，并加以论述，你是怎样计算出这棵大树的高度的(请画出示意图，并标明测量的数据，数据用a，b，……表示，并进行论证)。