八、解答题（本题8分）

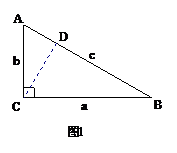
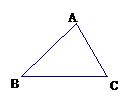
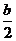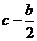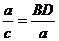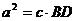他继续研究，在图1中，做斜边上的高CD，由于∠B=30°，可知c=2b，∠ACD=30°.于是AD= ，BD=.因为∠ACB=∠CDB=90°，∠B=∠B，所以△CDB∽△ACB，可知，即.同理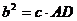.于是a²-b²=c（BD-AD）=c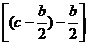=c（c-b）=c（2b-b）=bc.对于图2，由勾股定理知，a²=b²+c²，由于b=c，有a²-b²= bc.这两块三角板都具有a²-b²= bc性质.那么任意一个倍角三角形都有这个性质吗？

请解答下面的问题

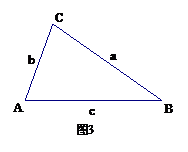
（1）       如图3，在△ABC中，∠CAB=2∠ABC，求证：a²-b²= bc；

（2）       若一个倍角三角形的三条边的长恰为三个连续的正整数，则这三条边的长为______________.（直接写出答案，不需说明理由）

23.在△ABC中如果一个内角等于另一个内角的2倍，我们称这个三角形为倍角三角形.小明在观察两块三角板（如图1、2）时发现，这两个三角形都是倍角三角形.

（图③）                                     （图④）

　解答问题：

（1）设图②中矩形ABCD和矩形AEFB的面积分别为S₁、S₂， 则S₁_____S₂（填“＞”，“＝”或“＜”）.　　

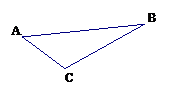
（2）如图③，△ABC是钝角三角形，按短文中的要求把它补成矩形，那么符合要求的矩形可以画出_____个，利用图③把它画出来.

（3）如图④，△ABC是锐角三角形且三边满足BC＞AC＞AB，按短文中的要求把它补成矩形，那符合要求的矩形可以画出____个，利用图④把它画出来.

（4）在（3）中所画出的矩形中，哪一个的周长最小？

七、解答题（本题6分）

（图①）                                           （图②）

21.已知直线l平分∠xoy，△ABC与△A₁B₁C₁关于直线l对称.

（1）在所给的直角坐标系中作出△A₁B₁C₁的图形；

（2）设点A的坐标是（4，2），求点A₁的坐标；

（3）设BC所在的直线的解析式是y=2x－4，求B₁C₁边所在直线的解析式.