25．(本题12分)如图①，在平面直角坐标系中，Rt△AOB≌Rt△CDA，且A(－1，0)、B(0，2)，抛物线y＝ax²＋ax－2经过点C。

(1)如图①，若∠BAC＝60°，则∠AFB＝_________；如图②，若∠BAC＝90°，则∠AFB＝_________；

(2)如图③，若∠BAC＝α，则∠AFB＝_________(用含α的式子表示)；

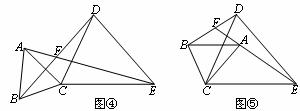
(3)将图③中的△ABC绕点C旋转(点F不与点A、B重合)，得图④或图⑤。在图④中，∠AFB与∠α的数量关系是________________；在图⑤中，∠AFB与∠α的数量关系是________________。请你任选其中一个结论证明。

24．(本题10分)填空或解答：点B、C、E在同一直线上，点A、D在直线CE的同侧，AB＝AC，EC＝ED，∠BAC＝∠CED，直线AE、BD交于点F。

23．(本题10分)康乐公司在A、B两地分别有同型号的机器17台和15台，现要运往甲地18台，乙地14台。从A、B两地运往甲、乙两地的费用如下表：

甲地(元/台)

乙地(元/台)

A地

600

500

B地

400

800

(1)如果从A地运往甲地x台，求完成以上调运所需总费用y(元)与x(台)的函数关系式；

(2)若康乐公司请你设计一种最佳调运方案，使总的费用最少，该公司完成以上调运方案至少需要多少费用？为什么？

22．(本题8分)如图，等腰三角形ABC中，AC＝BC＝10，AB＝12。以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E。

(1)求证：直线EF是⊙O的切线；

(2)求sin∠E的值。

(2)若将得分转化为等级，规定得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”。这次全区七年级参加竞赛的学生约有多少学生参赛成绩被评为“D”？如果随机抽查一名参赛学生的成绩等级，则这名学生的成绩被评为“A”、“B”、“C”、“D”哪一个等级的可能性大？请说明理由。

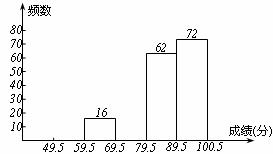
请你根据不完整的频率分布表，解答下列问题：

(1)补全频数分布直方图；

0.36