
22..如图1,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点P是对角线BD上的一点,PQ∥BA交AD于点Q,PS∥BC交DC于点S,四边形PQRS是平行四边形。
(1)当点P与点B重合时,图1变为图2,若∠ABD=90°,求证:△ABR≌△CRD;
当n=3时,钉子板上所连不同线段的长度值只有1,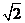 ,2,
,2,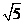 ,2
,2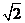 五种,比n=2时增加了3种,即S=2+3=5。
五种,比n=2时增加了3种,即S=2+3=5。
(1) 观察图形,填写下表:
钉子数(n×n)
S值
2×2
2
3×3
2+3
4×4
2+3+( )
5×5
( )
(2) 写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可)
(3)对n×n的钉子板,写出用n表示S的代数式。
七、(本题满分 12 分)
当n=2时,钉子板上所连不同线段的长度值只有1与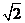 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
21.探索n×n的正方形钉子板上(n是钉子板每边上的钉子数),连接任意两个钉子所得到的不同长度值的线段种数:
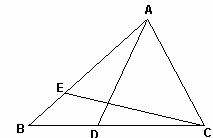
⑴求AE和BD的长;
⑵若∠BAC=90°,△ABC的面积为S,求证:S=AE?BD
六、(本题满分 12 分)
20.如图,DE分别是△ABC的边BC和AB上的点,△ABD与△ACD的周长相等,△CAE与△CBE的周长相等。设BC=a,AC=b,AB=c。
19.如图,某幢大楼顶部有一块广告牌CD,甲乙两人分别在相距 ≈1.73,计算结果保留整数)
≈1.73,计算结果保留整数)
18.据报道,我省农作物秸杆的资源巨大,但合理利用量十分有限,2006年的利用率只有30%,大部分秸杆被直接焚烧了,假定我省每年产出的农作物秸杆总量不变,且合理利用量的增长率相同,要使2008年的利用率提高到60%,求每年的增长率。(取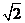 ≈1.41)
≈1.41)
五、(本题共2小题,每小题10分,满分20分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com