练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    中华人民共和国国旗上五角星的画法是，先把圆五等份，然后再连接五等分点，五角星的每一个角是______度．

    36 【解析】如图． ∵A、B、C、D、E是圆的五等分点， ∴， ∴每一条弧的度数都是360°÷5=72°， ∴∠CAD=∠EBD=∠ACE=∠BDA=∠CEB=72°÷2=36°， 即五角星每一个角的度数是36°， 故答案为：36.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年西藏拉萨市九年级（上）第一次月考数学试卷 题型：单选题

    平面直角坐标系中，点P的坐标为（﹣5，3），则点P关于原点对称的点的坐标是（　　）

    A. （5，﹣3） B. （﹣5，﹣3） C. （3，﹣5） D. （﹣3，5）

    A 【解析】根据中心对称的性质，可知：点A(－5，3)关于原点对称的点的坐标为(5，－3)．故选：A．

    查看答案和解析>>

    科目：初中数学 来源：广东省江门市江海区五校2017-2018学年七年级上学期期末联考数学试卷 题型：填空题

    如图所示是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形

    组成，…，第 10个图案中的基础图形个数为_____．

    31 【解析】试题分析：第1个图案基础图形的个数为4， 第2个图案基础图形的个数为7，7＝4＋3， 第3个图案基础图形的个数为10，10＝4＋3×2， …， 第n个图案基础图形的个数为4＋3（n-1）＝3n＋1， n＝10时，3n＋1＝31， 故答案为：31．

    查看答案和解析>>

    科目：初中数学 来源：2017年陕西省西安市中考数学模拟试卷 题型：解答题

    ①已知：△ABC中，BC=m，∠A=60°．问满足此条件的三角形有多少个？它们的最大面积存在吗？若存在求出最大面积，并回答此时三角形的形状；若不存在，请说明理由．

    ②有一个正方形的养鱼塘，四个角各有一棵大树．生产队设想把鱼塘扩大，使它成为一个面积最大的正方形，而又不把树挖掉，这一设想能否实现？若能，请你设计画出图形，并证明此时面积最大．若不能，请说明理由．

    ③上问题推广，有一个正五边形的养鱼塘，五个角各有一棵树，要扩大使它成为面积最大的正五边形，而又不把树挖掉，可以吗？画图说明．

    ①见解析；②见解析；③见解析. 【解析】试题分析：①根据A一定在以BC为弦，BC一侧，所对的圆周角是60°的圆上，当AB=AC时，△ABC的面积最大，据此即可求解； ②过各顶点作对应的对角线的垂线，各条线组成的四边形，就是所求的四边形； ③过各个顶点作正五边形，使各顶点时正五边形的各边的中点． 试题解析：①在△ABC中，BC=m，∠A=60°满足此条件的三角形有无数个； ...

    查看答案和解析>>

    科目：初中数学 来源：2017年陕西省西安市中考数学模拟试卷 题型：填空题

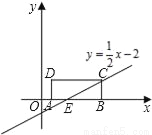
    如图，矩形ABCD的边长AB=9，AD=3，将此矩形置于平面直角坐标系xOy中，使AB在x轴正半轴上，经过点C的直线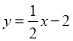与x轴交于点E，则四边形AECD的面积是_____．

    18 【解析】∵矩形ABCD的边长AB=9，AD=3的矩形， ∴S矩形ABCD=3×9=27， ∵经过点C的直线与x轴交于点E， ∴E（4，0），C（10，3）， ∴BE=6， ∴S△EBC=BE•BC==9， ∴四边形AECD的面积是：27﹣9=18， 故答案为：18．

    查看答案和解析>>

    科目：初中数学 来源：2017年陕西省西安市中考数学模拟试卷 题型：单选题

    已知实数x满足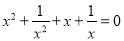，那么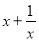的值是（　　）

    A. 1或﹣2 B. ﹣1或2 C. 1 D. ﹣2

    D 【解析】∵x2+=0 ∴（x+）2-2+x+=0， ∴[（x+）+2][（x+）﹣1]=0， ∴x+=1或﹣2． ∵x+=1无解， ∴x+=﹣2． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：2017学年第一学期上海（闵行区）九年级数学质量调研试卷 题型：解答题

    如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，CD是斜边上中线，点E在边AC上，点F在边BC上，且∠EDA=∠FDB，联结EF、DC交于点G．

    （1）当∠EDF=90°时，求AE的长；

    （2）CE = x，CF = y，求y关于x的函数关系式，并指出x的取值范围；

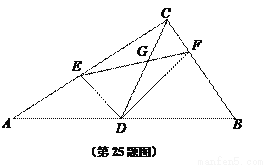
    （3）如果△CFG是等腰三角形，求CF与CE的比值．

    （1）；（2）；（3）. 【解析】试题分析： 过点E作EH⊥AB于点H，设DH=EH=a，tan∠A=， 得出AH= .在Rt△ABC中，根据勾股定理求出的值，进而求出.根据AH+HD=AD， 即可求得. 分别过点E、F作AB的垂线垂足为H、M，根据CE=x，CF=y，得出AE=4x，CF=3y．进而得到， ． ， ． ， ．根据tan∠EDA=tan∠FDB．即可得到函数...

    查看答案和解析>>

    科目：初中数学 来源：2017学年第一学期上海（闵行区）九年级数学质量调研试卷 题型：填空题

    已知两个相似三角形的相似比为2︰5，其中较小的三角形面积是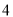，那么另一个三角形的面积为 ．

    25 【解析】试题解析：∵两个相似三角形的相似比为2:5， ∴面积的比是4:25， ∵小三角形的面积为4， ∴大三角形的面积为25. 故答案为：25.

    查看答案和解析>>

    科目：初中数学 来源：2017学年度第一学期上海（杨浦区）期末考试初三数学试卷 题型：填空题

    如图，Rt△ABC中，∠C=90°，M是AB中点，MH⊥BC，垂足为点H，CM与AH交于点O，如果AB=12，那么CO=_______．

    4. 【解析】试题解析：有题意可知： 故答案为：

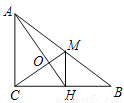
    查看答案和解析>>

    同步练习册答案