
科目: 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列选项正确的是
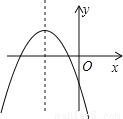
A.a>0 B.c>0 C.ac>0 D.bc<0
C 【解析】 试题分析:根据图象: 由抛物线开口向下得a<0, 根据对称轴在y轴左侧得到a与b同号得b<0, 由抛物线与y轴交点在负半轴得c<0。 因此,ac>0,bc>0。 故选C。查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
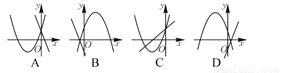
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
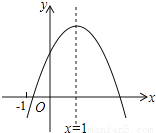
A.abc<0 B.2a+b=0 C.b2﹣4ac>0 D.a﹣b+c>0
D 【解析】 试题分析:A、由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,由a与0的关系并结合抛物线的对称轴判断b与0的关系,即可得出abc与0的关系; B、由抛物线的对称轴为x=1,可得﹣=1,再整理即可; C、利用抛物线与x轴的交点的个数进行分析即可; D、由二次函数的图象可知当x=﹣1时y<0,据此分析即可. 【解析】 A、由...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
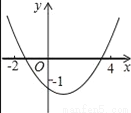
A. c>﹣1 B. b>0 C. 2a+b≠0 D. 9a+c>3b
D 【解析】由抛物线与y轴的交点在点(0,﹣1)的下方得到c<﹣1;由抛物线开口方向得a>0,再由抛物线的对称轴在y轴的右侧得a、b异号,即b<0;根据抛物线的对称性得到抛物线对称轴为直线x=﹣,若x=1,则2a+b=0,故可能成立;由于当x=﹣3时,y>0,所以9a﹣3b+c>0,即9a+c>3b. 【解析】 ∵抛物线与y轴的交点在点(0,﹣1)的下方. ∴c<﹣1; ...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac; ②4a-2b+c<0; ③不等式ax2+bx+c>0的解集是x≥3.5; ④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )

A. ①② B. ①④ C. ①③④ D. ②③④
B 【解析】试题分析:根据抛物线与x轴有两个交点可得b2﹣4ac>0,进而判断①正确; 根据题中条件不能得出x=﹣2时y的正负,因而不能得出②正确; 如果设ax2+bx+c=0的两根为α、β(α<β),那么根据图象可知不等式ax2+bx+c>0的解集是x<α或x>β,由此判断③错误; 先根据抛物线的对称性可知x=﹣2与x=4时的函数值相等,再根据二次函数的增减性即可判断④正...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是 ( )
A. 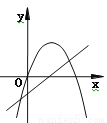 B.
B. 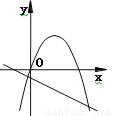
C. 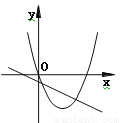 D.
D. 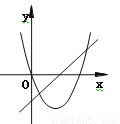
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
已知二次函数y=kx2-7x-7的图象与x轴有两个交点,则k的取值范围为( )
A. k>-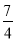 B. k<-
B. k<-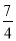 且k≠0
且k≠0
C. k≥-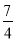 D. k>-
D. k>-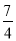 且k≠0
且k≠0
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0其中正确结论的有( )
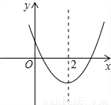
A. ①②③ B. ①②④ C. ①③④ D. ②③④
B 【解析】试题分析:由二次函数的图象开口向上可得a>0,根据二次函数的图象与y轴交于正半轴知:c>0,由对称轴直线x=2,可得出b与a异号,即b<0,则abc<0,故①正确; 把x=﹣1代入y=ax2+bx+c得:y=a﹣b+c,由函数图象可以看出当x=﹣1时,二次函数的值为正,即a﹣b+c>0,则b<a+c,故②选项正确; 把x=2代入y=ax2+bx+c得:y=4a+2b+...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=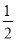 ,且经过点(2,0).下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(-2,y1),(
,且经过点(2,0).下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(-2,y1),(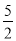 ,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
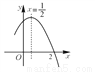
A. ①②④ B. ③④ C. ①③④ D. ①②
A 【解析】【解析】 ①∵二次函数的图象开口向下,∴a<0,∵二次函数的图象交y轴的正半轴于一点,∴c>0,∵对称轴是直线x=,∴ =,∴b=﹣a>0,∴abc<0. 故①正确; ②∵由①中知b=﹣a,∴a+b=0,故②正确; ③把x=2代入y=ax2+bx+c得:y=4a+2b+c,∵抛物线经过点(2,0),∴当x=2时,y=0,即4a+2b+c=0. 故③错误;...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
B 【解析】 试题分析:根据抛物线的对称轴为直线x=﹣=2,则有4a+b=0;观察函数图象得到当x=﹣3时,函数值小于0,则9a﹣3b+c<0,即9a+c<3b;由于x=﹣1时,y=0,则a﹣b+c=0,易得c=﹣5a,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;由于对称轴为直线x=2,根据二次函数的性质得到当x>2时...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com