
科目: 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:解答题
有一位旅客携带了30kg重的行李从上海乘飞机去北京,按民航总局规定:旅客最多可免费携带20kg重的行李,超重部分每千克按飞机票价格1.5%购买行李票,现该旅客购买了180元的行李票,则飞机票价格应是多少元?
飞机票价格应是1200元. 【解析】试题分析:设飞机票价格应是x元,根据该旅客购买了180元的行李票,列方程求解. 试题解析:【解析】 设飞机票价格应是x元,由题意得:(30﹣20)×1.5% x=180,解之得:x=1200. 答:飞机票价格应是1200元.查看答案和解析>>
科目: 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:解答题
A、B两站相距300千米,一列快车从A站开出,行驶速度是每小时60千米,一列慢车从B站开出,行驶速度是每小时40千米,快车先开15分钟,两车相向而行,快车开出几小时后两车相遇?(只列出方程,不用解)
. 【解析】试题分析:等量关系:快车行驶的路程+慢车行驶的路程=两车相距的路程,设快车开出x小时后两车相遇,快车行驶的路程为:60x千米,慢车行驶的路程为:40(x-)千米,根据题意可列出方程. 试题解析:设快车开出x小时后两车相遇, 根据题意得: .查看答案和解析>>
科目: 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:解答题
抗洪救灾小组在甲地段有28人,乙地段有15人,现在又调来29人,分配在甲乙两个地段,要求调配后甲地段人数是乙地段人数的2倍,求应调至甲地段和乙地段各多少人?
应调至甲地段20人,则调至乙地段9人 【解析】【解析】 设应调至甲地段x人,则调至乙地段(29-x)人-----1分 根据题意得 28+x=2(15+29-x) ------2分 解得 x=20 -------2分 经检验,符合题意 所以 29-x=9 ------1分 答:应调至甲地段20人,则调至乙地段9人 --------1分查看答案和解析>>
科目: 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:解答题
一份试卷,一共30道选择题,答对一题得3分,答错一题扣1分,小红每题都答了,共得78分,那么小红答对了几道题?请根据题意,列出方程.
3x-(30-x)×1=78. 【解析】等量关系为:答题得分=答对的题得分-答错题扣的分,设答对了x道题,则答错了(30-x)道题,答对题得分为:3x,答错的题扣分为: (30-x),根据题意可列出方程. 试题解析:设小红答对了x道题,由题意得: 3x-(30-x)×1=78.查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
下列方程中,是一元二次方程的是( )
A. 2x-y=3 B. x2+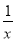 =2 C. x2+1=x2-1 D. x(x-1)=0
=2 C. x2+1=x2-1 D. x(x-1)=0
查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是( )
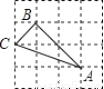
A. 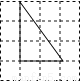 B.
B.  C.
C. 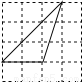 D.
D. 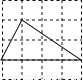
查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )
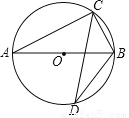
A. 130° B. 65° C. 35° D. 25°
D 【解析】试题分析:先根据圆周角定理得出∠ACB=90°,∠A=∠D,再由∠ABC=65°可得出∠A的度数,进而可得出结论. 【解析】 ∵AB是O的直径, ∴∠ACB=90°. ∵∠ABC=65°, ∴∠D=∠A=90°?65°=25°. 故选D.查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC = 4,那么CD的长为
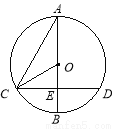
A.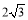 B.4 C.
B.4 C.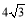 D.8
D.8
查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
关于x的一元二次方程(m﹣1)x2+2x+m2﹣5m+4=0,常数项为0,则m值等于( )
A. 1 B. 4 C. 1或4 D. 0
B 【解析】由题意,得m2﹣5m+4=0,且m﹣1≠0,解得m=4, 故选B.查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
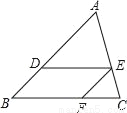
A. 6 B. 8 C. 10 D. 12
C 【解析】∵DE∥BC, ∴∠ADE=∠B,∠AED=∠C, 又∵∠ADE=∠EFC, ∴∠B=∠EFC,△ADE∽△EFC, ∴BD∥EF,, ∴四边形BFED是平行四边形, ∴BD=EF, ∴,解得:DE=10. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com