
科目: 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:填空题
计算:(1)15°30′5″=_________;
(2)30.26°=__________.
55805″ 30°15′36″ 【解析】【解析】 (1)15°30′5″=15×3600+30×60+5=55805″; (2)30.26°=30°+0.26×60′=30°15.6′=30°15′+0.6×60″=30°15′36″. 故答案为:(1).55805″; (2) 30°15′36″.查看答案和解析>>
科目: 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:填空题
如图,已知C为线段AB的中点,D在线段CB上.若DA=6,DB=4,则CD=________.
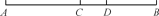
查看答案和解析>>
科目: 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:填空题
如图,OM平分∠AOB,ON平分∠COD.若∠MON=50°,∠BOC=10°,则∠AOD= __________.
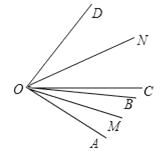
查看答案和解析>>
科目: 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:填空题
如图所示,由泰山到青岛的某一次列车,运行途中停靠的车站依次是:泰山﹣﹣济南﹣﹣淄博﹣﹣潍坊﹣﹣青岛,那么要为这次列车制作的火车票有 ________种.

查看答案和解析>>
科目: 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
按要求作图:如图,在同一平面内有四个点A、B、C、D.
①画射线CD;②画直线AD;③连结AB;④直线BD与直线AC相交于点O.
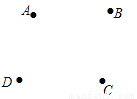
查看答案和解析>>
科目: 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
已知在平面内,∠AOB=70°,∠BOC=40°,求∠AOC的度数.
110°或30°. 【解析】试题分析:分两种情况考虑:(1)当∠BOC在∠AOB外部时;(2)当∠BOC在∠AOB内部时,分别求出∠AOC的度数即可. 试题解析:【解析】 分两种情况考虑: (1)当∠BOC在∠AOB外部时,∠AOC=∠AOB+∠BOC═70°+40°=110°; (2)当∠BOC在∠AOB内部时,∠AOC=∠AOB﹣∠BOC═70°﹣40°=30°,则∠...查看答案和解析>>
科目: 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
如图,直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
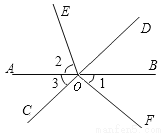
查看答案和解析>>
科目: 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
如图,已知点C为线段AB上一点,AC=12cm, CB=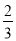 AC,D、E分别为AC、AB的中点,求线段DE的长。
AC,D、E分别为AC、AB的中点,求线段DE的长。
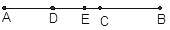
查看答案和解析>>
科目: 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
如图,在直线上任取1个点,2个点,3个点,4个点:

(1)填写下表:
点的个数 | 所得线段的条数 | 所得射线的条数 |
1 | 0 | 2 |
2 | 1 | 4 |
3 | 3 | 6 |
4 | 6 | 8 |
(2)在直线上取n个点,可以得到几条线段,几条射线?
(1)见解析;(2)条线段,2n条射线. 【解析】试题分析:(1)根据图形数出线段和射线的数量即可; (2)根据(1)中的数量,找出规律条线段,2n条射线. 【解答】【解析】 (1) 点的个数 所得线段的条数 所得射线的条数 1 0 2 2 1 4 3 3 6 4 6 8 (2)可以...查看答案和解析>>
科目: 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图1.
①若∠AOC=60°,求∠DOE的度数;
②若∠AOC=α,直接写出∠DOE的度数(用含α的式子表示);
(2)将图1中的∠DOC绕点O顺时针旋转至图2的位置,试探究∠DOE和∠AOC的度数之间的关系,写出你的结论,并说明理由.
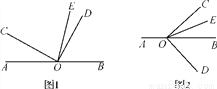
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com