
科目: 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )
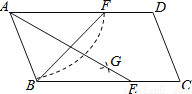
A.16 B.15 C.14 D.13
A 【解析】 试题分析:首先证明四边形ABEF是菱形,得出AE⊥BF,OB=OF=6,OA=OE,利用勾股定理计算出AO,从而得到AE的长. 【解析】 连结EF,AE与BF交于点O,如图, ∵AO平分∠BAD, ∴∠1=∠2, ∵四边形ABCD为平行四边形, ∴AF∥BE, ∴∠1=∠3, ∴∠2=∠3, ∴AB=EB, 同理:A...查看答案和解析>>
科目: 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使点C与点A重合,则折痕EF的长是( )
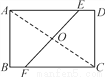
A. 7.5 B. 6 C. 10 D. 5
A 【解析】试题分析:根据矩形的性质可得AC=10,根据折叠图形可得AE=FC=AF,AO=CO=5,然后设AE=x,则BF=8-x,根据直角△ABF的勾股定理求出x的值,然后计算EF的长度.查看答案和解析>>
科目: 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )
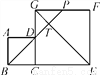
A. 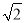 B. 2
B. 2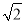 C. 2 D. 1
C. 2 D. 1
查看答案和解析>>
科目: 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
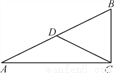
如图,在Rt△ABC中,∠ACB=90°,AB=10 cm,D为AB的中点,则CD=____________ cm.
查看答案和解析>>
科目: 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
已知(x-y+3)2+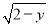 =0,则x+y=________.
=0,则x+y=________.
查看答案和解析>>
科目: 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
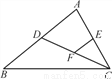
如图,CD是△ABC的中线,点E,F分别是AC,DC的中点,EF=1,则BD=____________.
查看答案和解析>>
科目: 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
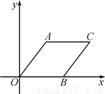
如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则菱形的周长为____________,点B的坐标是____________.
查看答案和解析>>
科目: 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
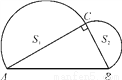
如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2等于____________.
查看答案和解析>>
科目: 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
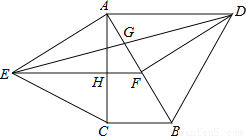
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=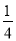 BD
BD
其中正确结论的为______(请将所有正确的序号都填上).
查看答案和解析>>
科目: 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:解答题
计算:
(1)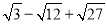 ; (2)(
; (2)(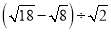 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com