
科目: 来源:2017年贵州省中考数学二模试卷 题型:填空题
观察下列等式:

在上述数字宝塔中,从上往下数,2016在第_____层.
44 【解析】试题分析:首先得出每一层的第一个数字为,每一行数的个数为2n+1个,然后根据规律得出答案.查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:填空题
(2010•沈阳)如图,在?ABCD中,点E在边BC上,BE:EC=1:2,连接AE交BD于点F,则△BFE的面积与△DFA的面积之比为 .
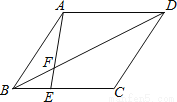
查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:填空题
如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为 .
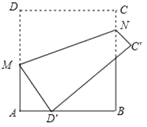
查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:解答题
计算:
(1)计算:(﹣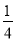 )﹣1﹣|﹣
)﹣1﹣|﹣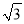 |﹣20110+(
|﹣20110+(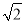 )2+tan60°;
)2+tan60°;
(2)解分式方程: 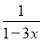 ﹣
﹣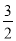 =
=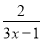 .
.
查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:解答题
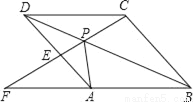
如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.
试问:(1)图中△APD与哪个三角形全等?并说明理由.
(2)求证:PA2=PE•PF.
查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:解答题
我省某地区为了了解2016年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如图1,如图2)
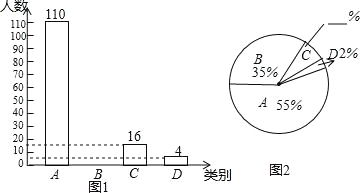
(1)填空:该地区共调查了 名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2016年初中毕业生共有3500人,请估计该地区今年初中毕业生中读普通高中的学生人数;
(4)老师想从甲,乙,丙,丁4位同学中随机选择两位同学了解他们毕业后的去向情况,请用画树状图或列表的方法求选中甲同学的概率.
(1)200;(2)详见解析;(3)1925;(4). 【解析】 试题分析:(1)根据统计图可以得到本次调查的九年级学生数;(2)根据题目中的数据可以得到统计图中未知的数据,从而可以解答本题;(3)根据统计图中的数据可以估计该地区今年初中毕业生中读普通高中的学生人数;(4)根据题意可以画出相应的树状图,从而可以求得选中甲同学的概率. 试题解析:(1)该地区调查的九年级学生数为:1...查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:解答题
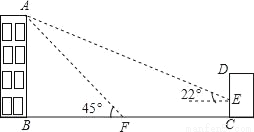
如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上)
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22°≈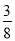 ,cos22°≈
,cos22°≈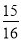 ,tan22°≈
,tan22°≈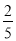 )
)
查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:解答题
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E. ⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=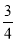 .
.
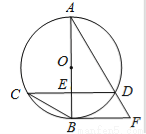
(1)求证:CD∥BF;
(2)求⊙O的半径;
(3)求弦CD的长.
(1)见解析(2)2(3) 【解析】【解析】 (1)∵BF是⊙O的切线 ∴AB⊥BF …………………1分 ∵AB⊥CD ∴CD∥BF………………………………………………2分 (2)连结BD ∵AB是直径 ∴∠ADB=90° ………………………………………3分 ∵∠BCD=∠BAD cos∠BCD=…………………4分 ∴cos∠BAD= 又∵AD=3...查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:解答题
某校组织学生到外地进行社会实践活动,共有680名学生参加,并携带300件行李.学校计划租用甲、乙两种型号的汽车共20辆.经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李.
(1)如何安排甲、乙两种汽车可一次性地将学生和行李全部运走?有哪几种方案?
(2)如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案.
①租用甲型汽车8辆、乙型汽车12辆;②租用甲型汽车9辆、乙型汽车11辆; ③租用甲型汽车10辆、乙型汽车10辆.(2)最省钱的租车方案是:租用甲型汽车8辆、乙型汽车12辆. 【解析】试题分析:(1)首先根据题意列出不等式组得 解出的取值范围,最后确定的取值,进而确定出具体方案; (2)首先求出关于租车总费用的函数关系式,再根据一次函数的增减性确定总费用最小的租车方案. 试...查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:解答题
如图,已知抛物线y=x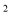 -ax+a
-ax+a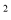 -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
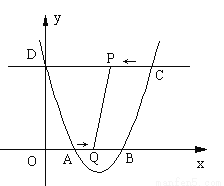
(1)求a的值;(2)当四边形ODPQ为矩形时,求这个矩形的面积;(3)当四边形PQBC的面积等于14时,求t的值.(4)当t为何值时,△PBQ是等腰三角形?(直接写出答案)
(1)8(2)(3)(4) 【解析】【解析】 (1)∵抛物线y=x-ax+a-4a-4经过点(0,8) ∴a-4a-4=8 解得:a=6,a=-2(不合题意,舍去) ∴a的值为6 (2)由(1)可得抛物线的解析式为 y=x-6x+8 当y=0时,x-6x+8=0 解得:x=2,x=4 ∴A点坐标为(2,0),B点坐标为(4,0) 当y=...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com