通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的。下面是一个案例，请补充完整。

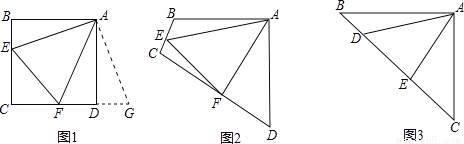
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由。

（1）思路梳理

∵AB=CD，

∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合。

∵∠ADC=∠B=90°，

∴∠FDG=180°，点F、D、G共线。

根据___________，易证△AFG≌__________，得EF=BE+DF。请写出完整证明过程。

（2）类比引申

如图2，四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°。

若∠B、∠D都不是直角，则当∠B与∠D满足等量关系_____________时，仍有EF=BE+DF。

（3）联想拓展

如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°。猜想BD、DE、EC应满足的等量关系，并写出推理过程。

（1）SAS，△AFE（2）∠B+∠D=180°（3）猜想：DE2=BD2+EC2 【解析】试题分析：（1）把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，再证明△AFG≌△AFE进而得到EF=FG，即可得EF=BE+DF； （2）∠B+∠D=180°时，EF=BE+DF，与（1）的证法类同； （3）根据△AEC绕点A顺时针旋转90°得到△ABE′，根据旋转的性质...

如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．

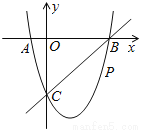
（1）求这个二次函数的表达式．

（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．

（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．

（1）y=x2-2x-3；（2）点P（，-）；（3）当x=时，四边形ABPC的面积最大．此时P点的坐标为（，-），四边形ABPC的面积． 【解析】试题分析：（1）将B、C的坐标代入抛物线的解析式中即可求得待定系数的值； （2）由于菱形的对角线互相垂直平分，若四边形POP′C为菱形，那么P点必在OC的垂直平分线上，据此可求出P点的纵坐标，代入抛物线的解析式中即可求出P点的坐标； （...

抛物线y＝－(x＋2)2－3的顶点坐标是

A. （－2，－3） B. （2，－3）

C. （2，3 ） D. （－2，3）

A 【解析】分析：已知解析式为顶点式，可直接根据顶点式的坐标特点，求顶点坐标，从而得出对称轴． 解答：【解析】 y=-（x+2）2-3是抛物线的顶点式， 根据顶点式的坐标特点可知，顶点坐标为（-2，-3）． 故答案为A．

下列四个图形分别是四届国际数学家大会的会标，其中属于中心对称图形的有( )

A. 1个 B. 2个 C. 3个 D. 4个

B 【解析】试题分析：根据中心对称的概念可得第一个图形是中心对称图形，第二个图形不是中心对称图形，第三个图形是中心对称图形，第四个图形不是中心对称图形，所以，中心对称图有2个．故选B．

下列事件中，是必然事件的是（　 　）

A. 抛掷一枚质地均匀的硬币，落地后正面朝上

B. 某人身高达到5.5米

C. 通常加热到100°C时，水沸腾

D. 打开电视，正在播放综艺节目《一站到底》

C 【解析】A. 抛掷一枚质地均匀的硬币，落地后正面朝上，随机事件；B. 某人身高达到5.5米，不可能事件；C. 通常加热到100°C时，水沸腾，必然事件；D. 打开电视，正在播放综艺节目《一站到底》，随机事件， 故选C.

若x=-1是方程x2+ax+2=0的一个根，则该方程的另一个根为（　 　）

A. 2 B. -2 C. 1 D. -1

B 【解析】设另一个根为x1，由根与系数关系则有：-1·x1=2，所以x1=-2， 故选B.

如果P（a-1，a+2）在x轴上，那么点P的坐标是（　 　）

A. （-3，0） B. （0，3） C. （0，-3） D. （3，0）

A 【解析】∵P（a-1，a+2）在x轴上，∴a+2=0，∴a=-2， ∴a-1=-2-1=-3， ∴点P的坐标是（-3，0）， 故选A.

如图，⊙O的弦AB=6，半径OD⊥AB，交AB于点D、交弧AB于点C．若CD=1，则⊙O的半径为（　 　）

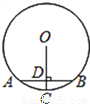
A. 4 B. 5 C. 6 D. 7

B 【解析】连接OA， ∵AB=6，OC⊥AB于点D， ∴AD=AB=×6=3，∠ADO=90°， ∴OD2= OA2-AD2， ∵CD=1，OA =OC ， ∴OD=OC-CD=OA-1, ∴（OA-1）2=OA2-32， ∴OA=5， 故选B.

在学校组织的实践活动中，小新同学用纸板制作了一个圆锥模型，它的底面半径为1，高为2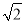，则这个圆锥的侧面积是（　 　）

A. 3π B. 4π C. 2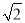π D. 2π

A 【解析】∵底面半径为1，高为2 ， ∴母线长==3， ∴圆锥的侧面积为：S侧=πrl=1×π×3=3π， 故选A．

抛物线y=ax2+bx+c中，a＞0，b＞0，c＜0，则抛物线的顶点在（　 　）

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

C 【解析】∵a>0，b>0， ∴a，b同号，抛物线的开口向上， ∴对称轴在y轴的左侧， ∵c<0， ∴抛物线与y轴的交点在x轴下方， ∴顶点在第三象限， 故选C．