
科目: 来源:2017年湖北省武汉市中考数学模拟试卷 题型:填空题
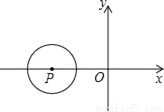
如图所示,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为 .
查看答案和解析>>
科目: 来源:2017年湖北省武汉市中考数学模拟试卷 题型:填空题
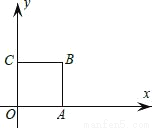
如图,在平面直角坐标系xOy中,正方形OABC的边长为2.写出一个函数y=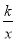 (k≠0),使它的图象与正方形OABC有公共点,这个函数的表达式为 .
(k≠0),使它的图象与正方形OABC有公共点,这个函数的表达式为 .
查看答案和解析>>
科目: 来源:2017年湖北省武汉市中考数学模拟试卷 题型:填空题
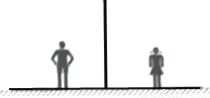
如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为 m.
查看答案和解析>>
科目: 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
先化简,再求代数式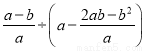 的值,其中
的值,其中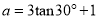 ,
, 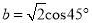 .
.
查看答案和解析>>
科目: 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
如图,AB=DC,AC=DB,求证:AB∥CD.
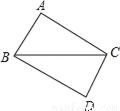
查看答案和解析>>
科目: 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图:
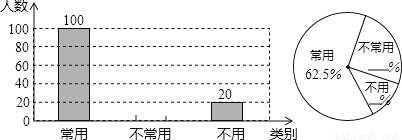
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是 ;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
【解析】 (1)160。 (2)不常用计算器的人数为:160﹣100﹣20=40; 不常用计算器的百分比为:40÷160=25%, 不用计算器的百分比为:20÷160=12.5%. 条形统计图和扇形统计图补全如下: (3)∵“不常用”计算器的学生数为40,抽查的学生人数为160, ∴从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是:。 ...查看答案和解析>>
科目: 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
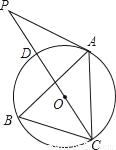
如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
(1)求证:AP是⊙O的切线;
(2)求PD的长.
查看答案和解析>>
科目: 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 ,x2 ,且x12+x22=10,求实数a的值.
(1)证明见解析;(2)a的值为﹣2+ 或﹣2﹣. 【解析】【试题分析】 (1)欲证明方程总有两个不相等的实数根,只需证明根的判别式大于0即可. △=(a+3)2﹣4(a+1)=a2+6a+9﹣4a﹣4=a2+2a+5=(a+1)2+4>0,从而得证; (2)根据韦达定理,将x12+x22=10转化为两根之和与两根之积的形式,代入得到关于a的方程,从而求出a即可. x12+x22...查看答案和解析>>
科目: 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
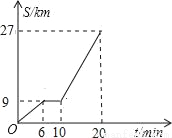
如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题:
(1)汽车在前6分钟内的平均速度是 千米/小时,汽车在兴国服务区停了多长时间? 分钟;
(2)当10≤t≤20时,求S与t的函数关系式;
(3)规定:高速公路时速超过120千米/小时为超速行驶,试判断当10≤t≤20时,该汽车是否超速,说明理由.
查看答案和解析>>
科目: 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
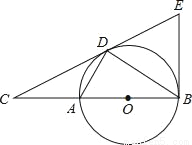
如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求∠BEC的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com