
科目: 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
如图,四边形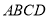 内接于⊙
内接于⊙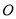 ,
, 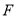 是弧
是弧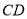 上一点,且弧
上一点,且弧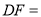 弧
弧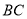 ,连接
,连接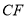 并延长交
并延长交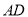 的延长线于点
的延长线于点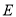 ,连接
,连接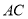 ,若
,若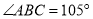 ,
, 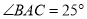 ,则
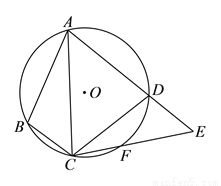
,则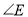 的度数为( ).
的度数为( ).
A. 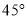 B.
B. 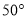 C.
C. 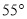 D.
D. 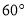
查看答案和解析>>
科目: 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
小方发现电线杆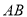 的影子落在土坡的坡面
的影子落在土坡的坡面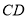 和地面
和地面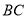 上,量得
上,量得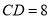 米,
米, 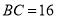 米,
米, 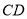 与地面成
与地面成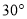 角,且此时测得
角,且此时测得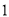 米杆的影长为
米杆的影长为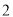 米,则电线杆
米,则电线杆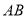 的高度为( ).
的高度为( ).

A. 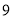 米 B.
米 B. 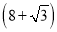 米 C.
米 C. 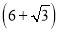 米 D.
米 D. 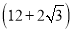 米
米
查看答案和解析>>
科目: 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
已知抛物线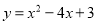 与
与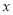 轴相交于点
轴相交于点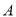 ,
,  (点
(点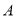 在点
在点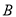 的左侧),顶点为
的左侧),顶点为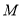 .平移该抛物线,使点
.平移该抛物线,使点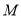 平移后的对应点
平移后的对应点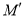 落在
落在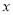 轴上,点
轴上,点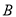 平移后的对应点
平移后的对应点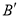 落在
落在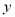 轴上,则平移后的抛物线的解析式为( ).
轴上,则平移后的抛物线的解析式为( ).
A. 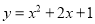 B.
B. 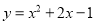 C.
C. 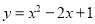 D.
D. 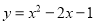
查看答案和解析>>
科目: 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
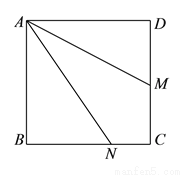
如图,正方形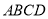 中,
中, 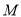 为
为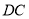 的中点,
的中点, 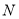 为
为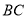 上一点,
上一点, 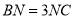 ,设
,设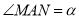 ,则
,则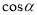 的值等于( ).
的值等于( ).
A. 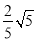 B.
B. 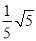 C.
C. 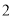 D.
D. 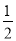
查看答案和解析>>
科目: 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
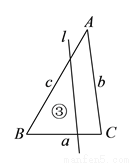
如图,已知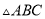 的三边长为
的三边长为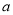 ,
, 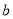 ,
, 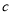 ,且
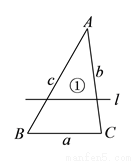
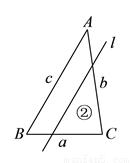
,且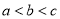 ,若平行于三角形一边的直线
,若平行于三角形一边的直线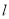 将
将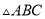 的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为
的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为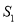 、
、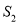 、
、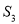 ,则
,则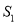 、
、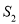 、
、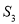 的大小关系是( ).
的大小关系是( ).
A. 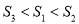 B.
B. 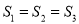 C.
C. 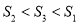 D.
D. 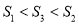
查看答案和解析>>
科目: 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
已知一个正多边形的一个外角的余弦值为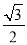 ,那么它是__________边形.
,那么它是__________边形.
查看答案和解析>>
科目: 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
在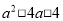 的空格□中,任意填上“+”或“-”,在所有得到的代数式中,能构成完全平方式的概率是__________.
的空格□中,任意填上“+”或“-”,在所有得到的代数式中,能构成完全平方式的概率是__________.
查看答案和解析>>
科目: 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
如图,任两个竖直或水平相邻的点都相距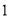 个单位长度.已知线段
个单位长度.已知线段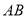 交线段
交线段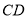 于点
于点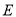 ,则线段
,则线段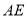 的长是__________.
的长是__________.

查看答案和解析>>
科目: 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
如图, 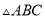 内接于⊙
内接于⊙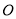 ,
, 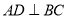 于点
于点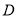 ,
, 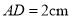 ,
, 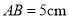 ,
, 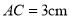 ,则⊙
,则⊙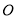 的直径是__________.
的直径是__________.

查看答案和解析>>
科目: 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
设二次函数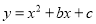 ,当
,当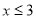 时,总有
时,总有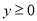 ,当
,当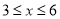 时,总有
时,总有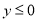 ,则
,则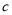 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com