相关习题
0 319995 320003 320009 320013 320019 320021 320025 320031 320033 320039 320045 320049 320051 320055 320061 320063 320069 320073 320075 320079 320081 320085 320087 320089 320090 320091 320093 320094 320095 320097 320099 320103 320105 320109 320111 320115 320121 320123 320129 320133 320135 320139 320145 320151 320153 320159 320163 320165 320171 320175 320181 320189 366461
科目:
来源:江苏省无锡市2018届九年级12月月考数学试卷
题型:填空题
已知圆锥的底面半径为3cm,母线为5cm,则这个圆锥的侧面积为________cm2.
15π
【解析】圆锥的侧面积=×2π×3×5=15π.
故答案为:15π.
查看答案和解析>>
科目:
来源:江苏省无锡市2018届九年级12月月考数学试卷
题型:填空题
某商场销售额3月份为16万元,5月份为25万元,设商场这两个月销售额的平均增长率为x,则可列方程为____________.
【解析】试题分析:3月份的销售额为16万元,平均每次增长百分率为x,则四月份的销售额是16(1+x),五月份的销售额是16(1+x)(1+x)即16(1+x)2,根据5月份的销售额是25万元可列方程为16(1+x)2=25.
故答案为:16(1+x)2=25.
查看答案和解析>>
科目:
来源:江苏省无锡市2018届九年级12月月考数学试卷
题型:填空题
如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,AB=20.则OE=_______.
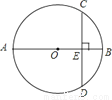
8
【解析】试题分析:∵直径AB=20,
∴半径为10,
连接OC,
∵AB为⊙O的直径,弦CD⊥AB于E,CD=12,
∴CE=DE=6,
由勾股定理得:OC2=CE2+OE2,
102=62+OE2,
∴OE=8,
故答案为8.
查看答案和解析>>
科目:
来源:江苏省无锡市2018届九年级12月月考数学试卷
题型:填空题
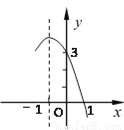
抛物线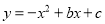 的部分图象如图所示,若
的部分图象如图所示,若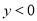 ,则
,则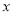 的取值范围是_______.
的取值范围是_______.
或
【解析】试题分析:根据图象可以知抛物线的对称轴为x=-1,根据抛物线的对称性可以确定抛物线与x轴的另一个交点横坐标为x=-3,y<0即对应抛物线在x轴下方部分,所以结合图象可得y<0时x的取值范围为x<-3或x>1.
故答案为x<-3或x>1.
查看答案和解析>>
科目:
来源:江苏省无锡市2018届九年级12月月考数学试卷
题型:填空题
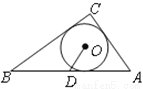
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O为△ABC 的内切圆,点D是斜边AB的中点,则tan∠ODA=_______.
2
【解析】试题分析:连接OE,OF,OG;
∵∠C=90°,AC=6,BC=8,
∴AB=10,
∵⊙O为△ABC的内切圆,
∴OG⊥BC,OF⊥AC,OE⊥AB,AF=AE,CF=CG,
∴∠OGC=∠OFC=∠OED=90°;
∵∠C=90°,
∴四边形OFCG是矩形,
∵OG=OF,
∴四边形OFCG是正方形;
设OF=x,...
查看答案和解析>>
科目:
来源:江苏省无锡市2018届九年级12月月考数学试卷
题型:填空题
边长为2的正方形ABCD与边长为2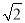 的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________
的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________ 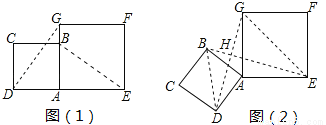
6
【解析】试题分析:)∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,AG=AE,∠DAB=∠EAG=90°,
∴∠DAB+∠BAG =∠EAG+∠BAG,
∴∠DAG=∠BAE,
∴△ADG≌△ABE(SAS),
∴∠AGD=∠AEB,
在正方形AEFG中,∠AGE=∠AEG=45°,
∴∠HGE+∠HEG=45°+∠AGD+45°-...
查看答案和解析>>
科目:
来源:江苏省无锡市2018届九年级12月月考数学试卷
题型:填空题
查看答案和解析>>
科目:
来源:江苏省无锡市2018届九年级12月月考数学试卷
题型:解答题
计算:(1)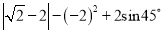 ; (2)
; (2)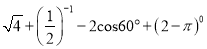
(1)-2;(2)4.
【解析】试题分析:(1)先化简绝对值,计算乘方,代入特殊角的三角函数值计算,然后合并同类二次根式即可;
(1)先计算算术平方根,负指数幂,代入特殊角的三角函数值,计算0次幂,最后相加减即可.
试题解析:
【解析】
(1)原式==-2;
(2)原式=2+2-2×+1=4-1+1=4.
查看答案和解析>>
科目:
来源:江苏省无锡市2018届九年级12月月考数学试卷
题型:解答题
(1)解方程: 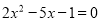 ; (2)
; (2)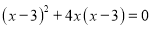
(1);(2).
【解析】试题分析:(1)直接利用公式法求解即可;
(2)利用因式分解法求解.
试题解析:
【解析】
(1),
a=2,b=-5,c=-1,
b2-4ac=(-5)2-4×2×(-1)=33>0,
,
∴;
(2),
(x-3)(x-3+4x)=0,
x-3=0或5x-3=0,
∴.
查看答案和解析>>
科目:
来源:江苏省无锡市2018届九年级12月月考数学试卷
题型:解答题
已知关于x的方程x2﹣(2m+1)x+m(m+1)=0,
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两根分别为x1、x2,求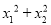 的最小值.
的最小值.
(1)证明见解析;(2)的最小值为.
【解析】试题分析:(1)根据方程的系数结合根的判别式,即可得出△=1>0,由此即可证出方程总有两个不相等的实数根;
(2)根据根与系数的关系可得x1+x2=2m+1、x1•x2=m(m+1),利用配方法可将x12+x22变形为(x1+x2)2-2 x1•x2,代入数据即可得出x12+x22=2(m+)2+,进而即可得出x12+x22的最小值.
...
查看答案和解析>>


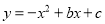 的部分图象如图所示,若
的部分图象如图所示,若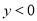 ,则
,则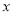 的取值范围是_______.
的取值范围是_______.

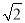 的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________
的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________ 
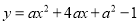 ,当
,当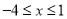 时,
时, 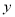 的最大值为5,则实数
的最大值为5,则实数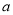 的值为_______.
的值为_______.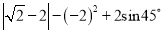 ; (2)
; (2)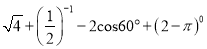
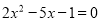 ; (2)
; (2)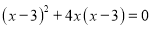
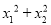 的最小值.
的最小值.