
科目: 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:解答题
如图所示,在菱形ABCD中,点E,F分别在CD,BC上,且CE=CF,求证:AE=AF.
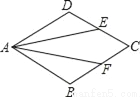
查看答案和解析>>
科目: 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:解答题
某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
(1)平均数为320件,中位数是210件,众数是210件;(2)不合理,定210件 【解析】试题分析:(1)根据平均数、中位数和众数的定义即可求得结果; (2)把月销售额320件与大部分员工的工资比较即可判断. (1)平均数件, ∵最中间的数据为210, ∴这组数据的中位数为210件, ∵210是这组数据中出现次数最多的数据, ∴众数为210件; (...查看答案和解析>>
科目: 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:解答题
已知关于x的一元二次方程ax2+x﹣a=0(a≠0).
(1)求证:对于任意非零实数a,该方程恒有两个异号的实数根;
(2)设x1、x2是该方程的两个根,若|x1|+|x2|=4,求a的值.
(1)证明见解析(2)a=± 【解析】试题分析:(1)求证对于任意非零实数a,该方程恒有两个异号的实数根,即证明一元二次方程的根的判别式△=b2-4ac>0,则方程有两个不相等的实数根,若两根之积小于0,则方程有两个异号的实数根; (2)根据一元二次方程的根与系数的关系得到,两根之和与两根之积,把|x1|+|x2|=4变形成与两根之和与两根之积有关的式子,代入两根之和与两根之积,求得a...查看答案和解析>>
科目: 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:解答题
某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是6时,它也不一定是正多边形,如图1,△ABC是正三角形, 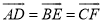 ,证明六边形ADBECF的各内角相等,但它未必是正六边形.
,证明六边形ADBECF的各内角相等,但它未必是正六边形.
丙同学:我能证明,边数是5时,它是正多边形,我想…,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图2)是正七边形;(不必写已知,求证)
(3)根据以上探索过程,提出你的猜想.(不必证明)
查看答案和解析>>
科目: 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:解答题
某中学为筹备校庆活动,准备印制一批校庆纪念册。该纪念册每册需要10张8K大小的纸,其中4张为彩页,6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩页300元/张,黑白页50元/张;印刷费与印数的关系见下表。
印数a (单位:千册) | 1≤a<5 | 5≤a<10 |
彩色 (单位:元/张) | 2.2 | 2.0 |
黑白(单位:元/张) | 0.7 | 0.6 |
①印制这批纪念册的制版费为 元;
②如果印制2千册,则共需费用 元;
③如果该校希望印数至少为4千册,总费用至多为60000元,求印数的取值范围。(精确到0.01千册)
①1500元②27500 元③5.00≤a≤5.04(千册) 【解析】 试题分析:①制版费=4×300+6×50=1500(元) ②总费用=2000(4×2.2+6×0.)+1500=27500 元 ③(1)当4000≤a<5000时(4×2.2+6×0.7)a+1500≤60000 4.00≤a≤4.50(千册) (2)当5000≤a<10000时(4×2+6...查看答案和解析>>
科目: 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:解答题
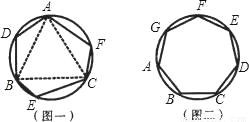
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
(1)P点的坐标为多少;(用含x的代数式表示)
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果.
查看答案和解析>>
科目: 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:解答题
已知:如图,点A在y轴上,⊙A与x轴交于B、C两点,与y轴交于点D(0,3)和点E(0,﹣1)
(1)求经过B、E、C三点的二次函数的解析式;
(2)若经过第一、二、三象限的一动直线切⊙A于点P(s,t),与x轴交于点M,连接PA并延长与⊙A交于点Q,设Q点的纵坐标为y,求y关于t的函数关系式,并观察图形写出自变量t的取值范围;
(3)在(2)的条件下,当y=0时,求切线PM的解析式,并借助函数图象,求出(1)中抛物线在切线PM下方的点的横坐标x的取值范围.
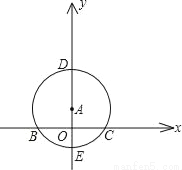
查看答案和解析>>
科目: 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:单选题
下列方程中有实数根的是( )
A. x2+2x+2=0 B. x2﹣2x+3=0 C. x2﹣3x+1=0 D. x2+3x+4=0
C 【解析】解:A.△=22﹣4×1×2=﹣6<0,则该方程无实数根,故本选项错误; B.△=(﹣2)2﹣4×1×3=﹣8<0,则该方程无实数根,故本选项错误; C.△=(﹣3)2﹣4×1×1=5>0,则该方程有实数根,故本选项正确; D.△=32﹣4×1×4=﹣7<0,则该方程无实数根,故本选项错误; 故选C.查看答案和解析>>
科目: 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:单选题
若x=3是方程x2﹣5x+m=0的一个根,则这个方程的另一个根是( )
A. ﹣2 B. 2 C. ﹣5 D. 5
B 【解析】试题解析:由根与系数的关系,设另一个根为x, 则3+x="5," 即x="2." 故选B.查看答案和解析>>
科目: 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:单选题
如图, AB是⊙O的直径,C,D为圆上两点,若∠AOC =130°,则∠D等于 ( )

A. 20° B. 25° C. 35° D. 50°
C 【解析】试题分析:∵AB是⊙O的直径, ∴∠BOC=180°-∠AOC=180°-130°=50°, ∴∠D=∠BOC=×50°=25°. 故选:C查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com