
科目: 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:填空题
已知函数y=(m+1)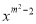 是反比例函数,则m的值为 .
是反比例函数,则m的值为 .
查看答案和解析>>
科目: 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:填空题
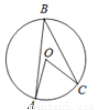
如图,点A,B,C在⊙O上,若∠ABC=40°,则∠AOC的度数为 _________ .
查看答案和解析>>
科目: 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:填空题
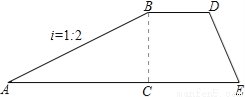
如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为 .
查看答案和解析>>
科目: 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:填空题
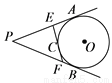
如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在上,若PA长为2,则△PEF的周长是__________.
查看答案和解析>>
科目: 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:填空题
在一幅长8分米,宽6分米的矩形风景画(如图①)的四周镶宽度相同的金色纸边,制成一幅矩形挂图(如图②).如果要使整个挂图的面积是80平方分米,求金色纸边的宽.设金色纸边的宽为x分米,请根据题意列出方程: .

查看答案和解析>>
科目: 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:解答题
计算题
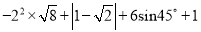
查看答案和解析>>
科目: 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:解答题
已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.
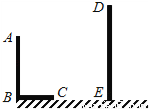
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
(1)作图见解析; (2)10m. 【解析】试题分析:(1)根据投影的定义,作出投影即可; (2)根据在同一时刻,不同物体的物高和影长成比例;构造比例关系AB:DE=BC:EF.计算可得DE=10(m). 试题解析:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影. (2)∵AC∥DF, ∴∠ACB=∠DFE. ∵∠ABC=∠DEF=...查看答案和解析>>
科目: 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:解答题
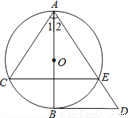
如图,AB为⊙O的直径,劣弧BC=劣弧BE,BD∥CE,连接AE并延长交BD于D.
求证:(1)AC=AE;
(2)AB2=AC•AD.
查看答案和解析>>
科目: 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:解答题
小美有红色、白色、蓝色上衣各一件,黄色、黑色长裤各一条.(1)请用画树状图或列表的方法分析小美上衣和长裤有多少种不同的搭配情况;(2)其中小美穿蓝色上衣的概率是多少?
(1)小美上衣和长裤有6种不同的搭配情况(2) 【解析】试题分析:(1)列出表格即可得小美上衣和长裤不同搭配的所有情况.(2)利用概率公式直接求解即可. 试题解析:(1)列表得, 红色 白色 蓝色 黄色 (红色,黄色) (白色,黄色) (蓝色,黄色) 黑色 (红色,黑色) ...查看答案和解析>>
科目: 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:解答题
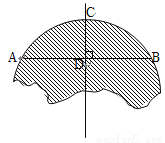
如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB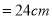 , CD
, CD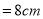 .
.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com