练习册

  • 练习册
  • 试题
    相关习题
     0  321932  321940  321946  321950  321956  321958  321962  321968  321970  321976  321982  321986  321988  321992  321998  322000  322006  322010  322012  322016  322018  322022  322024  322026  322027  322028  322030  322031  322032  322034  322036  322040  322042  322046  322048  322052  322058  322060  322066  322070  322072  322076  322082  322088  322090  322096  322100  322102  322108  322112  322118  322126  366461 

    科目： 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：填空题

    计算：(4a－b2)2=______________.

    16a2－8ab2＋b4 【解析】(4a?b2)2=（4a）2-2·4a·b2+( b2)2=16a2?8ab2+b4. 故答案为：16a2?8ab2+b4.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：填空题

    计算：20152－2×2015×2014＋20142=__.

    1 【解析】20152－2×2015×2014＋20142=(2015-2014)2=12=1. 故答案为：1.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：填空题

    已知P=3xy－8x＋1，Q=x－2xy－2，当x≠0时，3P－2Q=7恒成立，则y的值为__.

    2 【解析】∵P=3xy?8x+1，Q=x?2xy?2， ∴3P?2Q=3(3xy?8x+1)?2(x?2xy?2)=7恒成立， ∴9xy?24x+3?2x+4xy+4=7， 13xy?26x=0， 13x(y?2)=0， ∵x≠0， ∴y?2=0， ∴y=2； 故答案为：2.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：填空题

    如果a与b异号，那么(a＋b)2与(a－b)2的大小关系是___________________.

    (a＋b)2＜(a－b)2 【解析】(a+b)2?(a?b)2=a2+2ab+b2?(a2?2ab+b2=4ab， 而ab<0， ∴(a+b)2?(a?b)2<0. 故答案为：(a＋b)2＜(a－b)2.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：解答题

    计算：

    (1)m3·m2＋m7÷(－m2)＋(m2)3；

    (2)(x2－2xy)·9x2－(9xy3－12x4y2)÷3xy.

    (1) m6;(2) 9x4－14x3y－3y2 【解析】试题分析：（1）原式先利用单项式乘单项式、单项式除以单项式以及幂的乘方计算，再合并即可； （2）原式利用单项式乘以多项式，多项式除以单项式法则计算，去括号合并即可得到结果． 试题解析：（1）原式= m5-m5＋m6= m6； （2）原式=9x4-18x3y-3y2+4x3y=9x4－14x3y－3y2.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：解答题

    计算：

    (1)(3a＋5b－2c)(3a－5b－2c)；

    (2)(x＋1)(x2－1)(x－1)．

    (1) 9a2＋4c2－25b2－12ac;(2) x4－2x2＋1. 【解析】试题分析：（1）利用平方差公式进行计算即可； （2）原式先利用平方差公式再利用完全平方公式进行计算即可. 试题解析：（1）原式=[(3a－2c) ＋5b] [(3a－2c) －5b]= (3a－2c)2 －(5b)2=9a2＋4c2－25b2－12ac； （2）原式=(x＋1) (x－1) (x...

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：解答题

    如图，要设计一幅长为3xcm、宽为2ycm的长方形图案，其中有两横两竖的彩条，横彩条的宽度为acm，竖彩条的宽度为bcm，问空白区域的面积是多少？

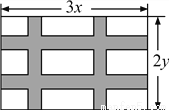
    6xy－6ax－4by＋4ab(cm2) 【解析】试题分析：此题可将彩条平移到如图所示的长方形的靠边处，则空白部分组成一个长方形，这个大长方形长（3x-2b）cm，宽为（2y-2a），则空白部分的面积=长×宽即可得出． 试题解析： 可设想将彩条平移到如图所示的长方形的靠边处，将9个小矩形组合成“整体”， 一个大的空白长方形，则该长方形的面积就是空白区域的面积. 而这个...

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：解答题

    试说明：两个连续奇数的积加上1，一定是一个偶数的平方．

    证明见解析. 【解析】试题分析：由题意设两个连续奇数为2n-1，2n+1，然后根据平方差公式进行证明． 试题解析：设两个连续奇数为2n?1，2n+1， 则(2n?1)(2n+1)+1=(2n)2?1+1=(2n)2 结果成立.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：解答题

    当x、y为何值时，代数式x2＋y2＋4x－6y＋15有最小值？并求出最小值．

    =－2，y=3时，代数式有最小值为2. 【解析】试题分析：本题将待求式变形为(x+2)2+(y?3)2+2,进而利用完全平方式的特征,问题即可迎刃而解. 试题解析：对代数式变形,得：(x2+4x+4)+(y2?6y+9)+2 由完全平方公式,得：(x+2)2+(y?3)2+2 观察上式发现：(x+2)2≥0，(y?3)2≥0 所以当x=-2,y=3时,待求式有最小值,...

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：解答题

    观察下列运算过程：

    S=1＋3＋32＋33＋…＋32014＋32015　①，

    ①×3，得

    3S=3＋32＋33＋…＋32015＋32016　②，

    ②－①，得

    2S=32016－1，S=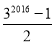

    运用上面计算方法计算：

    1＋5＋52＋53＋…＋52017的值．

    【解析】试题分析：观察题中所给的数字，首先设S=1+5+52+53+54+55+…+52016+52017；结合上式可得5S=5×(1+5+52+53+54+55+…+52017)，接下来两式相减，进行整理，即可解答本题. 试题解析：设S＝1＋5＋52＋53＋…＋52 017，① ①×5，得5S＝5＋52＋53＋54＋…＋52 018.② ②-①，得4S＝52 018-1， ...

    查看答案和解析>>

    同步练习册答案