相关习题
0 322127 322135 322141 322145 322151 322153 322157 322163 322165 322171 322177 322181 322183 322187 322193 322195 322201 322205 322207 322211 322213 322217 322219 322221 322222 322223 322225 322226 322227 322229 322231 322235 322237 322241 322243 322247 322253 322255 322261 322265 322267 322271 322277 322283 322285 322291 322295 322297 322303 322307 322313 322321 366461
科目:
来源:北师大版七年级数学下册4.3.3探索三角形全等的条件练习
题型:单选题
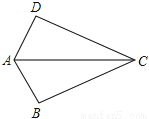
如图,已知AB=AD给出下列条件:
(1)CB=CD (2)∠BAC=∠DAC (3)∠BCA=∠DCA (4)∠B=∠D,
若再添一个条件后,能使△ABC≌△ADC的共有( )
A. 1个 B. 2个 C. 3个 D. 4个

B
【解析】∵在△ABC和△ADC中,AB=AD,AC=AC,
∴(1)添加“CB=CD”可由“SSS”判定△ABC≌△ADC;
(2)添加“∠BAC=∠DAC”可由“SAS”判定△ABC≌△ADC;
(3)添加“∠BCA=∠DCA”不能判定△ABC≌△ADC;
(4)添加“∠B=∠D”不能判定△ABC≌△ADC;
即4个条件中,添加(1)和(2)能使△ABC≌...
查看答案和解析>>
科目:
来源:北师大版七年级数学下册4.3.3探索三角形全等的条件练习
题型:单选题
如图,已知AB∥CD,AE=CF,则下列条件中不一定能使△ABE≌△CDF的是( )

A. AB=CD B. BE∥DF C. ∠B=∠D D. BE=DF

D
【解析】∵AB∥CD,
∴∠A=∠C,
又∵AE=CF,
∴(1)添加“AB=CD”,可由“SAS”判定△ABE≌△CDF;
(2)添加“BE∥DF”可得∠FEB=∠EFD,进一步可得∠AEB=∠CFD,从而可由“ASA”判定△ABE≌△CDF;
(3)添加“∠B=∠D”可由“AAS”判定△ABE≌△CDF;
(4)添加“BE=DF”不能判定△ABE≌...
查看答案和解析>>
科目:
来源:北师大版七年级数学下册4.3.3探索三角形全等的条件练习
题型:单选题
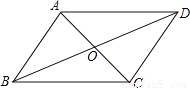
如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等( )
A. 1 B. 2 C. 3 D. 4

D
【解析】∵AC与BD相交于点O,
∴∠AOD=∠COB,∠AOB=∠COD,
又∵OA=OC,OB=OD,
∴△AOD≌△COB,△AOB≌△COD,
∴AD=CB,AB=CD,
又∵AC=CA,BD=DB,
∴△ACD≌△CAB,△ABD≌△CDB,
即图中共有4对全等三角形.
故选D.
查看答案和解析>>
科目:
来源:北师大版七年级数学下册4.3.3探索三角形全等的条件练习
题型:单选题
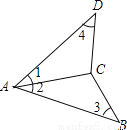
如图,下列条件能保证△ABC≌△ADC的是:①AB=AD,BC=DC;②∠1=∠3,∠4=∠2;③∠1=∠2,∠4=∠3;④∠1=∠2,AB=AD;⑤∠1=∠2,BC=DC.( )
A. ①②③④⑤ B. ①②③④ C. ①③④ D. ①③④⑤

C
【解析】∵在△ABC和△ADC中,AC=AC,
∴当添加条件:①AB=AD,BC=DC时,可由“SSS”得到△ABC≌△ADC;
当添加条件:②∠1=∠3,∠4=∠2时,不能得到△ABC≌△ADC;
当添加条件:③∠1=∠2,∠4=∠3时,可由“AAS”得到△ABC≌△ADC;
当添加条件:④∠1=∠2,AB=AD时,可由“SAS”得到△ABC≌△ADC;
...
查看答案和解析>>
科目:
来源:北师大版七年级数学下册4.3.3探索三角形全等的条件练习
题型:解答题
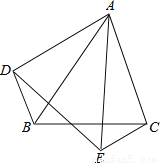
如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:BD=EC。

证明见解析
【解析】试题分析:
由∠BAC=∠DAE易得∠BAD=∠EAC,结合AB=AE,AC=AD,即可由“SAS”证得:△BAD≌△EAC,从而可得:BD=EC.
试题解析:
∵∠DAE=∠BAC,
∴∠DAE-∠BAE=∠EAC-∠BAE,
∴∠BAD=∠EAC,
在△BAD和△EAC中,
∴△BAD≌△EAC(SAS),
∴BD=EC...
查看答案和解析>>
科目:
来源:北师大版七年级数学下册4.3.3探索三角形全等的条件练习
题型:解答题
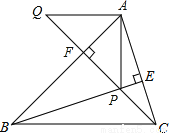
如图,BE、CF是△ABC的高且相交于点P,AQ∥BC交CF延长线于点Q,若有BP=AC,CQ=AB,线段AP与AQ的关系如何?说明理由。

证明见解析
【解析】试题分析:
由BE、CF是△ABC的高,易得∠ABP+∠BPF=90°,∠ACP+∠CPE=90°,结合∠BPF=∠CPE,易得∠ABP=∠ACP,这样结合BP=AC,CQ=AB,即可由“SAS”证得△ACQ≌△PBA,从而可得AP=AQ,∠Q=∠PAF,结合∠PAF+∠APF=90°,可得:∠APF+∠Q=90°,即可得到∠QAP=90°,从而可得AQ⊥AP,由此...
查看答案和解析>>
科目:
来源:北师大版七年级数学下册4.3.3探索三角形全等的条件练习
题型:解答题
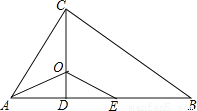
如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC。
(1)求证:△AOC≌△A0E;
(2)求证:OE∥BC。

(1)证明见解析(2)证明见解析
【解析】试题分析:
(1)由AO平分∠BAC,可得∠CAO=∠EAO结合AO=AO,AE=AC即可由“SAS”证得:△AOC≌△AOE;
(2)由△AOC≌△AOE可得∠ACO=∠AEO,由∠ACB=90°,CD⊥AB于点D,易得∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,从而可得∠DCB=∠DOE,即可得到:OE∥BC.
试题...
查看答案和解析>>
科目:
来源:北师大版七年级数学下册4.3.3探索三角形全等的条件练习
题型:解答题
如图1,四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC。
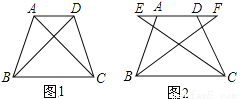
(1)求证:AC=DB;
(2)如图2,E、F两点同时从A、D出发在直线AD上以相同的速度反向而行,BF和CE会相等吗?请证明你的结论。

(1)证明见解析(2)BF=CE
【解析】试题分析:
(1)由∠ABC=∠DCB,AB=DC结合BC=CB即可证得:△ABC≌△DCB,从而可得AC=DB;
(2)由题意可得AE=DF,从而可得AF=DE,由AD∥BC结合∠ABC=∠DCB,易得∠BAD=∠CDA,再结合AB=DC即可证得△BAF≌△CDE,从而可得BF=CE.
试题解析:
(1)在△ABC和△DCB...
查看答案和解析>>
科目:
来源:北师大版七年级数学下册4.3.3探索三角形全等的条件练习
题型:解答题
如图,点B、D、E、C在一条直线上,△ABD≌△ACE,AB和AC,AD和AE是对应边,除△ABD≌△ACE外,图中还有其他全等三角形吗?若有,请写出来,并证明你的结论。
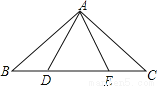

有,△ABE≌△ACD
【解析】试题分析:
由△ABD≌△ACE可得:AB=AC,BD=CE,∠B=∠C,从而易得BE=CD,这样由“SAS”即可证得△ABE和△ACD.
试题解析:
有,△ABE≌△ACD;理由如下:
∵△ABD≌△ACE,
∴AB=AC,BD=CE,∠B=∠C,
∴BE=CD,
在△ABE和△ACD中,
,
∴△ABE...
查看答案和解析>>
科目:
来源:北师大版七年级数学下册4.3.3探索三角形全等的条件练习
题型:解答题
如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,AC∥DE,延长CA交射线EB于点G,点F恰好是AD中点。
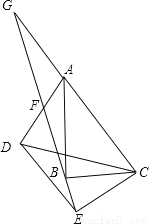
(1)求证:△AFG≌△DFE;
(2)若BC=CE,
①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。

(1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△A...
查看答案和解析>>


 C
【解析】∵在△ABC和△ADC中,AC=AC,
∴当添加条件:①AB=AD,BC=DC时,可由“SSS”得到△ABC≌△ADC;
当添加条件:②∠1=∠3,∠4=∠2时,不能得到△ABC≌△ADC;
当添加条件:③∠1=∠2,∠4=∠3时,可由“AAS”得到△ABC≌△ADC;
当添加条件:④∠1=∠2,AB=AD时,可由“SAS”得到△ABC≌△ADC;
...
C
【解析】∵在△ABC和△ADC中,AC=AC,
∴当添加条件:①AB=AD,BC=DC时,可由“SSS”得到△ABC≌△ADC;
当添加条件:②∠1=∠3,∠4=∠2时,不能得到△ABC≌△ADC;
当添加条件:③∠1=∠2,∠4=∠3时,可由“AAS”得到△ABC≌△ADC;
当添加条件:④∠1=∠2,AB=AD时,可由“SAS”得到△ABC≌△ADC;
...
 (1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△A...
(1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△A...