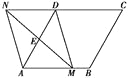
如图所示,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;

(2)①当AM为何值时,四边形AMDN是矩形?

②当AM为何值时,四边形AMDN是菱形?

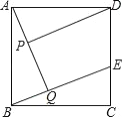
已知：如图，在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P．

（1）求证：AP=BQ；

（2）在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对中较长线段与较短线段长度的差等于PQ的长．

如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．

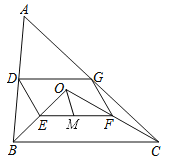
（1）求证：四边形DEFG是平行四边形；

（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．

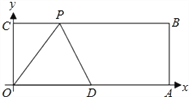
如图，已知O为坐标原点，四边形OABC为长方形，A（10，0），C（0，4），点D是OA的中点，点P在BC上运动．

（1）当△ODP是等腰三角形时，请直接写出点P的坐标；

（2）求△ODP周长的最小值．（要有适当的图形和说明过程）

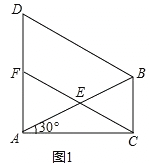
如图1，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，E是AB的中点，连接CE并延长交AD于F．

（1）求证：△AEF≌△BEC；

（2）判断四边形BCFD是何特殊四边形，并说出理由；

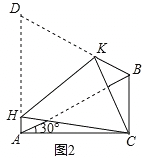
（3）如图2，将四边形ACBD折叠，使D与C重合，HK为折痕，若BC=1，求AH的长．

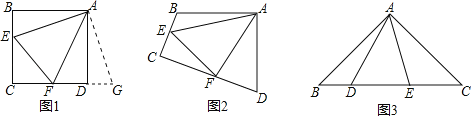
（1）探究：如图1和2，四边形ABCD中，已知AB=AD，∠BAD=90°，点E、F分别在BC、CD上，∠EAF=45°．

①如图1，若∠B、∠ADC都是直角，把△ABE绕点A逆时针旋转90°至△ADG，使AB与AD重合，则能证得EF=BE+DF，请写出推理过程；

②如图2，若∠B、∠D都不是直角，则当∠B与∠D满足数量关系 时，仍有EF=BE+DF；

（2）拓展：如图3，在△ABC中，∠BAC=90°，AB=AC=2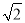，点D、E均在边BC上，且∠DAE=45°．若BD=1，求DE的长．

如图，在矩形ABCD中，AB=2，AD=．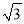

(1)在边CD上找一点E，使EB平分∠AEC，并加以说明；

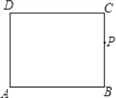
(2)若P为BC边上一点，且BP=2CP，连结EP并延长交AB的延长线于F．

①求证：AB=BF；

②△PAE能否由△PFB绕P点按顺时针方向旋转而得到?若能，加以证明，并写出旋转度数；若不能，请说明理由.

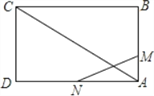
如图，已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻，动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：

（1）经过多少时间，△AMN的面积等于矩形ABCD面积的九分之一？

（2）是否存在时刻t，使以A,M,N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由．

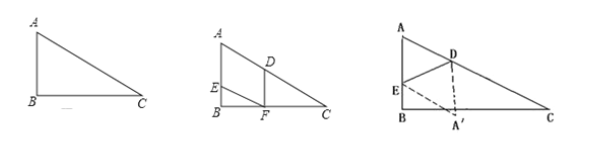
（本小题12分）如图1，已知在Rt△ABC中，∠ABC=90°，∠C=30°，AC=12cm，点E从点A出发沿AB以每秒1cm的速度向点B运动，同时点D从点C出发沿CA以每秒2cm的速度向点A运动，运动时间为t秒（0＜t＜6），过点D作DF⊥BC于点F．

（1）试用含t的式子表示AE、AD的长；

（2）如图2，在D、E运动的过程中，四边形AEFD是平行四边形，请说明理由；

（3）连接DE,当t为何值时，△DEF为直角三角形？

（4）如图3，连接DE，将△ADE沿DE翻折得到△A′DE，试问当t为何值时，四边形AEA′D为菱形？

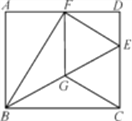
如图，在矩形ABCD中，点E为CD上一点，将△BCE沿BE翻折后点C恰好落在AD边上的点F处，将线段EF绕点F旋转，使点E落在BE上的点G处，连接CG.

(1)证明：四边形CEFG是菱形；

(2)若AB=8，BC=10，求四边形CEFG的面积；

(3)试探究当线段AB与BC满足什么数量关系时，BG=CG，请写出你的探究过程．