
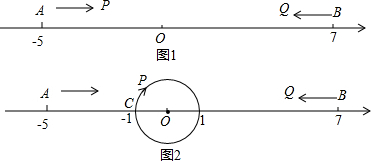
分析 (1)先求出点P从点A出发以每秒1个单位长度的速度向右运动,出发6s后,点P,Q的距离,再根据时间=距离和÷速度和,列出算式计算即可求解;
(2)①先求出P点到C的时间,再加上绕着圆旋转的数据即为所求;
②点P和点Q只能相遇在-1或1,分别求出它们在-1或1的时间即可求解;
③先求出点Q到1的时间,点Q到-1的时间,依此即可求解.
解答 解:(1)(7+5-6×1)÷(1+2)
=(12-6)÷3
=6÷3
=2(秒).
答:再经过2秒,两点相遇;
(2)①P在数轴上方时,t=360°÷60°n+(-1+5)÷1+90°÷60°=6n+5.5;
P在数轴下方时,t=360°÷60°n+(-1+5)÷1+(360°-90°)÷60°=6n+8.5;
故当t═(6n+5.5)s或(6n+8.5)s,其中n为非负整数时,∠AOP=90°;
②P在-1的时间是(6n+4)s,P在1的时间是(6n+7)s,
点Q在1的时间是3s,点Q在1的时间是4s,
当n=0时,点P和点Q会相遇.
③点Q在1的时间是(12n+3)s或(12n+9)s,点Q在-1的时间是(12n+4)s或(12n+8)s,
(110-4)÷12
=106÷12
=8…10(s),
1+8=9(次).
故当t=110s时,P、Q两点相遇了9次.
故答案为:(6n+5.5)s或(6n+8.5)s,其中n为非负整数.
点评 本题考查了数轴,主要利用了数轴上两点间的距离的求解,相遇问题的等量关系,难点在于(2)(3)要分情况讨论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
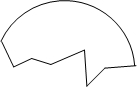 考古学家发现了一块古代圆形残片如图所示,为了修复这块残片,需要找出圆心.
考古学家发现了一块古代圆形残片如图所示,为了修复这块残片,需要找出圆心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com