在正方形ABCD中.点E是对角线AC的中点.点F在边CD上.连接DE.AF.点G在线段AF上(1)如图①.若DG是△ADFD的中线.DG=2.5.DF=3.连接EG.求EG的长,(2)如图②.若DG⊥AF交AC于点H.点F是CD的中点.连接FH.求证:∠CFH=∠AFD,(3)如图③.若DG⊥AF交AC于点H.点F是CD上的动点.连接EG．当点F在边CD上运动时.∠EGH的大小是否发生改变?若不改� 题目和参考答案——青夏教育精英家教网—

1．在正方形ABCD中，点E是对角线AC的中点，点F在边CD上，连接DE、AF，点G在线段AF上

（1）如图①，若DG是△ADFD的中线，DG=2.5，DF=3，连接EG，求EG的长；
（2）如图②，若DG⊥AF交AC于点H，点F是CD的中点，连接FH，求证：∠CFH=∠AFD；
（3）如图③，若DG⊥AF交AC于点H，点F是CD上的动点，连接EG．当点F在边CD上（不含端点）运动时，∠EGH的大小是否发生改变？若不改变，求出∠EGH的度数；若发生改变，请说明理由．

分析（1）由正方形的性质得出AD=CD=BC，∠ADF=∠BCD=90°，∠DAC=∠ACB=∠ACD=45°，由直角三角形斜边上的中线性质得出AF=2DG=5，由勾股定理求出CD=AD=4，得出CF=1，由三角形中位线定理得出EG=$\frac{1}{2}$CF=$\frac{1}{2}$即可；
（2）延长DH交BC于M，证出∠AFD=∠DMC，由AAS证明△CDM≌△DAF，得出对应边相等CM=DF，由已知条件得出DF=CF，因此CM=CF，由SAS证明△CMH≌△CFH，得出对应角相等∠CMH=∠CFH，即可得出结论；
（3）由直角三角形的性质得出DE=$\frac{1}{2}$AC=AE，由等腰三角形的性质得出∠ADE=∠DAC=45°，证出∠AED=90°=∠AGD，延长A、D、G、E四点共圆，由圆周角定理得出∠AGE=∠ADE=45°，即可得出结果．

解答（1）解：∵四边形ABCD是正方形，
∴AD=CD=BC，∠ADF=∠BCD=90°，∠DAC=∠ACB=∠ACD=45°，
∵DG是△ADF的中线，DG=2.5，
∴AF=2DG=5，
∴CD=AD=$\sqrt{A{F}^{2}-D{F}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴CF=CD-DF=1，
∵点E是对角线AC的中点，G是AF的中点，
∴EG是△ACF的中位线，
∴EG=$\frac{1}{2}$CF=$\frac{1}{2}$；
（2）证明：延长DH交BC于M，如图所示，
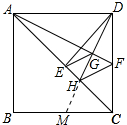
∵DG⊥AF，
∴∠AGH=∠DGA=∠DGF=90°，
∴∠AFD+∠FDG=90°，
∵∠DMC+∠FDG=90°，
∴∠AFD=∠DMC，
在△CDM和△DAF中，$\left\{\begin{array}{l}{∠BCD=∠ADF}&{\;}\\{∠DMC=∠AFD}&{\;}\\{CD=AD}&{\;}\end{array}\right.$，
∴△CDM≌△DAF（AAS），
∴CM=DF，
∵点F是CD的中点，
∴DF=CF，
∴CM=CF，
在△CMH和△CFH中，$\left\{\begin{array}{l}{CM=CF}&{\;}\\{∠HCM=∠HCF}&{\;}\\{CH=CH}&{\;}\end{array}\right.$，
∴△CMH≌△CFH（SAS），
∴∠CMH=∠CFH，
∴∠CFH=∠AFD；
（3）解：∠EGH的大小不发生改变，∠EGH=45°；理由如下：
∵点E是对角线AC的中点，∠ADC=90°，
∴DE=$\frac{1}{2}$AC=AE，
∴∠ADE=∠DAC=45°，
∴∠AED=90°=∠AGD，
∴A、D、G、E四点共圆，
∴∠AGE=∠ADE=45°，
∴∠EGH=90°-45°=45°．

点评本题是四边形综合题目，考查了正方形的性质、直角三角形斜边上的中线性质、勾股定理、三角形中位线定理、四点共圆、圆周角定理等知识；本题综合性强，有一定难度，特别是（2）中，需要证明两次三角形全等才能得出结论．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

3．中考男生1000米测试在3分40秒内可得满分．小明想得到满分，则他每分钟至少要跑多少米？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．将下列二次根式中根号外的因数或因式移至根号内．
（1）3$\sqrt{3}$；
（2）x$\sqrt{-x}$．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

9．

如图，四边形ABCD中，AB∥CD，点E是边AD上的点，BE平分∠ABC，CE平分∠BCD，有下列结论：①AD=AB+CD，②E为AD的中点，③BC=AB+CD，④BE⊥CE，其中正确的有②③④．（填序号）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

16．

如图，在平行四边形ABCD中，对角线AC与BD相交于点O，如果$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$．那么下列选项中，正确的是（　　）

A．

$\overrightarrow{OC}$=$\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$）

B．

$\overrightarrow{OA}$=$\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$）

C．

$\overrightarrow{OD}$=$\frac{1}{2}$（$\overrightarrow{a}$-$\overrightarrow{b}$）

D．

$\overrightarrow{BD}$=（$\overrightarrow{a}$-$\overrightarrow{b}$）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

已知数轴上，点O为原点，点A对应的数为9，点B对应的数为b，点C在点B右侧，长度为2个单位的线段BC在数轴上移动．
（1）如图1，当线段BC在O、A两点之间移动到某一位置时恰好满足线段AC=OB，求此时b的值；
（2）当线段BC在数轴上沿射线AO方向移动的过程中，若存在AC-OB=$\frac{1}{2}$AB，求此时满足条件的b值；
（3）当线段BC在数轴上移动时，满足关系式|AC-OB|=$\frac{7}{11}$|AB-OC|，则此时的b的取值范围是b≥-2或b＞9或b=$\frac{7}{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

13．若四边形ABCD的对角线交于点O，且有$\overrightarrow{AB}=2\overrightarrow{DC}$，则以下结论正确的是（　　）

A．

$\overrightarrow{AO}=2\overrightarrow{OC}$

B．

$|\overrightarrow{AC}|=|\overrightarrow{BD}|$

C．

$\overrightarrow{AC}=\overrightarrow{BD}$

D．

$\overrightarrow{DO}=2\overrightarrow{OB}$

查看答案和解析>>