
 已知数轴上,点O为原点,点A对应的数为9,点B对应的数为b,点C在点B右侧,长度为2个单位的线段BC在数轴上移动.
已知数轴上,点O为原点,点A对应的数为9,点B对应的数为b,点C在点B右侧,长度为2个单位的线段BC在数轴上移动.分析 (1)由题意可知B点表示的数比点C对应的数少2,进一步用b表示出AC、OB之间的距离,联立方程求得b的数值即可;
(2)分别用b表示出AC、OB、AB,进一步利用AC-0B=$\frac{1}{2}$AB建立方程求得答案即可;
(3)分别用b表示出AC、OB、AB、OC,进一步利用|AC-OB|=$\frac{7}{11}$|AB-OC|建立方程求得答案即可.
解答 解:(1)由题意得:
9-(b+2)=b,
解得:b=3.5.
答:线段AC=OB,此时b的值是3.5.
(2)由题意得:
①9-(b+2)-b=$\frac{1}{2}$(9-b),
解得:b=$\frac{5}{3}$.
②9-(b+2)+b=$\frac{1}{2}$(9-b),
解得:b=-5
答:若AC-0B=$\frac{1}{2}$AB,满足条件的b值是$\frac{5}{3}$或-5.
(3)①当b≥9时,AC=b+2-9,OB=b,AB=b-9,OC=b+2,
|AC-OB|=$\frac{7}{11}$|AB-OC|,
|b+2-9-b|=7,
$\frac{7}{11}$|AB-OC|=$\frac{7}{11}$×11=7,
∴恒成立;
②7≤b<9时,
|AC-OB|=$\frac{7}{11}$|AB-OC|,
|b+2-9-b|=$\frac{7}{11}$|9-b-(b+2)|,
解得b=-2(舍去)或b=9(舍去);
③0≤b<7时,
|AC-OB|=$\frac{7}{11}$|AB-OC|,
|9-(b+2)-b|=$\frac{7}{11}$|9-b-(b+2)|,
解得b=$\frac{7}{2}$=3.5.
④-2≤b<0时,
|9-(b+2)+b|=$\frac{7}{11}$|9-b-(b+2)|,
解得b=-2或b=9(舍去);
⑤当b<-2时,
|9-(b+2)+b|=$\frac{7}{11}$|9-b+(b+2)|恒成立,
综上,b的取值范围是b≤-2或b≥9或b=3.5.
点评 本题考查了一元一次方程的应用,考查了数轴与两点间的距离的计算,根据数轴确定出线段的长度是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$x | B. | x | C. | 6$\sqrt{2}$x | D. | $\frac{2\sqrt{2}}{3}$x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
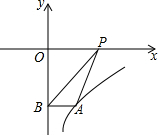 如图,点A是反比例函数y=-$\frac{4}{x}$的图象上一点,过点A作AB⊥y轴于点B,点P是x轴上的一个动点,则△ABP的面积为2.
如图,点A是反比例函数y=-$\frac{4}{x}$的图象上一点,过点A作AB⊥y轴于点B,点P是x轴上的一个动点,则△ABP的面积为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com