练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．解不等式：5（x-2）-2（x+1）＞3．

    分析 先去括号，再根据不等式的基本性质把不等号右边的x移到左边，合并同类项，化系数为1即可求得原不等式的解．

    解答 解：去括号得5x-10-2x-2＞3，
    移项得5x-2x＞3+10+2，
    合并同类项得3x＞15，
    化系数为1得x＞5．
    故原不等式的解集为：x＞5．

    点评 本题考查的是解一元一次不等式，在解答此类题目时一定要根据不等式的基本性质解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

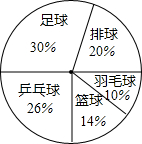    20．某学校七年级三班有50名学生，现对学生最喜欢的球类运动进行了调查，根据调查的结果制作了扇形统计图，如图所示．根据扇形统计图中提供的信息，给出以下结论，正确的是（　　）
    A．最喜欢足球的人数是15人B．最喜欢羽毛球的人数是4人
    C．最喜欢排球的人数是20人D．最喜欢乒乓球的人数是26人

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图，∠AOB的一边OA为平面镜，∠AOB=37°36′，在OB上有一点E，从E点射出一束光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB的度数是（　　）
    A．74°12′B．74°36′C．75°12′D．75°36′

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

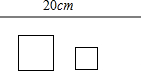    18．刘老师在数学课上给出了一个情景：如图，将一根长为20cm的铁丝剪成两段，以每一段为周长各围成一个正方形．
    （1）设较长的一段铁丝长为xcm，请计算出这两个正方形的面积之差；
    （2）是否存在合适的x的值，使两个正方形的面积刚好相差5cm2？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

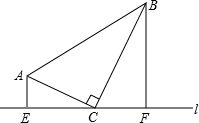    1．如图，Rt△ABC中，∠ACB=90°，直线l经过C点，AE⊥l交直线l于E点，BF⊥l交直线l于点F，若$\frac{{{S_{△ACE}}}}{{{S_{△CBF}}}}=\frac{4}{9}$，则$\frac{AC}{BC}$=$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

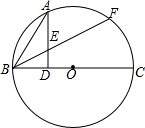    11．如图，BC是⊙O的直径，AD⊥BC于D，$\widehat{AB}$=$\widehat{AF}$，BF交AD于E
    （1）求证：AE=BE；
    （2）探究线段AB、BE、BF之间的数量关系，并证明；
    （3）若A、F把半圆BAC三等分，BC=12，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．先化简，再求值：$\frac{x+1}{x-2}$÷（x+2+$\frac{3}{x-2}$），其中x=$\sqrt{2}$-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

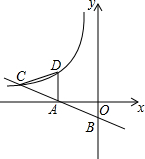    15．如图，直线y=-$\frac{1}{2}$x-1与x轴、y轴分别交于点A、B，与反比例函数y=$\frac{k}{x}$（x＜0）的图象交于点C，过点A作AD⊥0A，交反比例函数的图象于点D，连结CD．
    （1）若已知AB=AC，求反比例函数的表达式；
    （2）若已知CD=AC，求△ACD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知，在△ABC中，AB=AC，D为AB边上一点，过点D作DF∥AC交BC于F，过F作FE∥AB交AC于E．
    （1）如图1，当D为AB中点时，试判断四边形ADFE的形状；
    （2）如图2，当∠BAC=120°时，延长DF到G，使DF=FG，连接AF、AG、EG、CG，当AG=EF，AB=6时，求CG的长．

    查看答案和解析>>

    同步练习册答案