
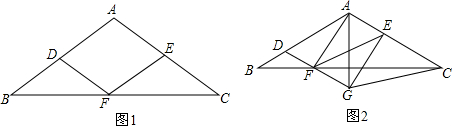
分析 此题分两种情况,①BC 是△ABC的底边,如图1,由已知条件得:AB=AC=10,BC=12,过A作AM⊥BC于M,交GF于N,根据等腰三角形的性质得到BM=$\frac{1}{2}$BC=6,AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=8,通过三角形相似得到比例式即可得到结果;
②BC 是△ABC的腰,如图2,由已知条件得:AC=BC=10,AB=12,过A作AM⊥BC于M,交GF于N,得到△AGF∽△ABC,在Rt△AMC与Rt△ABM中,根据勾股定理求得CM=$\frac{14}{5}$,得到AM=$\frac{48}{5}$,通过比例式列方程即可得到结果.
解答 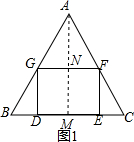 解:①BC 是△ABC的底边,如图1,
解:①BC 是△ABC的底边,如图1,
由已知条件得:AB=AC=10,BC=12,
过A作AM⊥BC于M,交GF于N,
∴BM=$\frac{1}{2}$BC=6,∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=8,
∵四边形DEFG是正方形,
∴GF∥DE,DG=GF=DE,
∴AN⊥GF,
∴△AGF∽△ABC,
∴$\frac{GF}{BC}=\frac{AN}{AM}=\frac{AM-GF}{AM}$,
∴$\frac{GF}{12}=\frac{8-GF}{8}$,
解得;GF=$\frac{24}{5}$;
②BC 是△ABC的腰,如图2,
由已知条件得:AC=BC=10,AB=12,
过A作AM⊥BC于M,交GF于N,
∵四边形DEFG是正方形,
∴GF∥DE,DG=GF=DE,
∴AN⊥GF,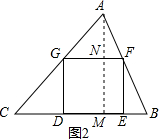
∴△AGF∽△ABC,
在Rt△AMC与Rt△ABM中,
AC2-CM2=AB2-BM2=AB2-(BC-CM)2,
即:102-CM2=122-(10-CM)2,
解得:CM=$\frac{14}{5}$,
∴AM=$\frac{48}{5}$,
∵△AGF∽△ABC,
∴$\frac{GF}{BC}=\frac{AN}{AM}=\frac{AM-GF}{AM}$,
即$\frac{GF}{10}=\frac{\frac{48}{5}-GF}{\frac{48}{5}}$,
解得;GF=$\frac{240}{49}$,
∴正方形DEFG的边长为:$\frac{24}{5}$或$\frac{240}{49}$,
故答案为:$\frac{24}{5}$或$\frac{240}{49}$.
点评 本题考查了相似三角形的判定和性质,正方形的性质,等腰三角形的性质,正确的作出图形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
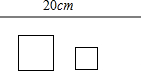 刘老师在数学课上给出了一个情景:如图,将一根长为20cm的铁丝剪成两段,以每一段为周长各围成一个正方形.
刘老师在数学课上给出了一个情景:如图,将一根长为20cm的铁丝剪成两段,以每一段为周长各围成一个正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
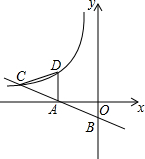 如图,直线y=-$\frac{1}{2}$x-1与x轴、y轴分别交于点A、B,与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点C,过点A作AD⊥0A,交反比例函数的图象于点D,连结CD.
如图,直线y=-$\frac{1}{2}$x-1与x轴、y轴分别交于点A、B,与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点C,过点A作AD⊥0A,交反比例函数的图象于点D,连结CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
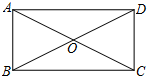 如图,在矩形ABCD中,AB=3,BC=6,对角线交于点O.将△BCD沿直线BD翻折,得到△BED.
如图,在矩形ABCD中,AB=3,BC=6,对角线交于点O.将△BCD沿直线BD翻折,得到△BED.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
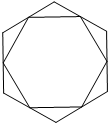 如图,顺次连接一个正六边形各边的中点,所得图形仍是正六边形.若大正六边形的面积为S1,小正六边形的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值是$\frac{4}{3}$.
如图,顺次连接一个正六边形各边的中点,所得图形仍是正六边形.若大正六边形的面积为S1,小正六边形的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值是$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
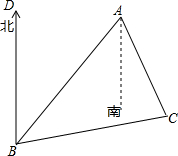 如图所示,B处在A处的南偏西45°方向上,C处在A处的南偏东30°方向,C处在B处的北偏东85°,求∠ACB是多少度?(提示:在三角形ABC中,∠BAC+∠ABC+∠ACB=180°)
如图所示,B处在A处的南偏西45°方向上,C处在A处的南偏东30°方向,C处在B处的北偏东85°,求∠ACB是多少度?(提示:在三角形ABC中,∠BAC+∠ABC+∠ACB=180°)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com