
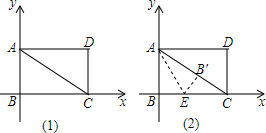
���� ��1���������֪��C��4��0����A��0��3������AC�Ľ���ʽΪy=kx+b������A��C���������õ�����k��b�Ķ�Ԫһ�η����飬�Ӷ������k��b��ֵ�����ǿɵõ�ֱ��AC�Ľ���ʽΪy=-$\frac{3}{4}$x+3��
��2����Rt��ABC�У��ɹ��ɶ��������AC=5���ɷ��۵����ʿ�֪����EB��C=90�㣬BE=BE�䣬B��C=2����BE=B��E=x��Ȼ����Rt��B��EC�У��ɹ��ɶ����г����ڹ���x�ķ��̣��Ӷ������BE=$\frac{3}{2}$��
��3������ͼ��1����ʾ������P��PF��AD������ΪF����S��ADP=2S��ABE�������PF=$\frac{9}{4}$���Ӷ��õ���P��������Py=4-$\frac{9}{4}$=$\frac{7}{4}$����y=$\frac{7}{4}$����y=-$\frac{3}{4}$x+3�����x=$\frac{5}{3}$���Ӷ��õ���P������Ϊ��$\frac{5}{3}$��$\frac{7}{4}$����
����ͼ��2����ʾ������P��PF��AD������ΪF���ɢٿ�֪��PF=$\frac{9}{4}$������õ�P��������Py=$\frac{25}{4}$����y=$\frac{25}{4}$����y=-$\frac{3}{4}$x+3�����x=-$\frac{13}{3}$�����ǵõ���P������Ϊ��-$\frac{13}{3}$��$\frac{25}{4}$����
��� �⣺��1����BC=4��AB=3��
��C��4��0����A��0��3����
��AC�Ľ���ʽΪy=kx+b������A��C���������ã�$\left\{\begin{array}{l}{4k+b=0}\\{b=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=-$\frac{3}{4}$x+3��
��2����Rt��ABC�У��ɹ��ɶ����ã�AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5��
���ɷ��۵����ʿ�֪��BE=B��E��AB=AB��=3����B=��AB��E=90��
��B��C=5-3=2����EB��C=90�㣮
��BE=B��E=x����EC=4-x��
��Rt��B��EC�У��ɹ��ɶ����ã�EC2=EB��2+B��C2������4-x��2=x2+22��
��ã�x=$\frac{3}{2}$��
��BE=$\frac{3}{2}$��
���E��������$\frac{3}{2}$��0����
��3������ͼ��1����ʾ������P��PF��AD������ΪF��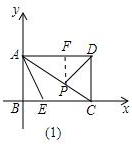
${S}_{��ABE}=\frac{1}{2}AB•BE$=$\frac{1}{2}��3��\frac{3}{2}$=$\frac{9}{4}$��
��S��ADP=2S��ABE��
��S��ADP=2��$\frac{9}{4}$=$\frac{9}{2}$��
��$\frac{1}{2}��AD•PF=\frac{9}{2}$����$\frac{1}{2}��4��PF=\frac{9}{2}$��
��ã�PF=$\frac{9}{4}$��
���P��������Py=4-$\frac{9}{4}$=$\frac{7}{4}$��
��y=$\frac{7}{4}$����y=-$\frac{3}{4}$x+3�ã�$-\frac{3}{4}x+3=\frac{7}{4}$��
��ã�x=$\frac{5}{3}$��
���P��������$\frac{5}{3}$��$\frac{7}{4}$����
����ͼ��2����ʾ������P��PF��AD������ΪF��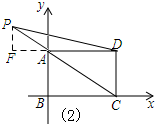
���ɢٿ�֪��PF=$\frac{9}{4}$��
���P��������Py=$\frac{9}{4}+4$=$\frac{25}{4}$��
��y=$\frac{25}{4}$����y=-$\frac{3}{4}$x+3�ã�-$\frac{3}{4}$x+3=$\frac{25}{4}$��
��ã�x=-$\frac{13}{3}$��
���P��������-$\frac{13}{3}$��$\frac{25}{4}$����
������������P��������$\frac{5}{3}$��$\frac{7}{4}$����-$\frac{13}{3}$��$\frac{25}{4}$����
���� ������Ҫ�������һ�κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ������һ�κ����Ľ���ʽ�����ɶ����������ε������ʽ��һ�κ���ͼ���ϵ�������ص㣬���ݵ�P���߶�AC�ϡ���P���߶�AC������ͼ���ǽ���Ĺؼ���


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������У�Ļ�У�ij��ȤС���������ͼ6��ʾ��ֱ��ǽ�ǣ�CD�����ڵ�ǽ��10�ף�DA�����ڵ�ǽ�㹻��������28�׳������Χ��һ�����λ�ABCD�����ֻΧAB��BC���ߣ�����AB=x�ף�
������У�Ļ�У�ij��ȤС���������ͼ6��ʾ��ֱ��ǽ�ǣ�CD�����ڵ�ǽ��10�ף�DA�����ڵ�ǽ�㹻��������28�׳������Χ��һ�����λ�ABCD�����ֻΧAB��BC���ߣ�����AB=x�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
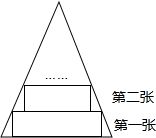 ��ͼ��ʾ��һ�ŵ���������ֽƬ���ױ߳�18cm���ױ��ϵĸ߳�18cm�����صױ������������ϲü����Ⱦ�Ϊ3cm�ľ���ֽ������֪���õ�ֽ������һ���������Σ�������������ֽ���ǣ�������
��ͼ��ʾ��һ�ŵ���������ֽƬ���ױ߳�18cm���ױ��ϵĸ߳�18cm�����صױ������������ϲü����Ⱦ�Ϊ3cm�ľ���ֽ������֪���õ�ֽ������һ���������Σ�������������ֽ���ǣ�������| A�� | ��4�� | B�� | ��5�� | C�� | ��6�� | D�� | ��7�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com