
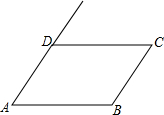
 如图所示:已知AD∥BC,∠A=∠C.
如图所示:已知AD∥BC,∠A=∠C.分析 (1)由平行线的性质得∠A+∠ABC=180°,又∠A=∠C,等量代换得∠C+∠ABC=180°,由同旁内角互补,两直线平行得出结论;
(2)由(1)中的∠ABC+∠C=180°和已知条件∠ABC-∠C=60°可得2∠C=120°,易得∠C.
解答 解:(1)AB∥CD,
∵AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=∠C,
∴∠C+∠ABC=180°,
∴AB∥DC;
(2)∵∠ABC-∠C=60°,∴∠ABC=∠C+60°,
由(1)知,∠ABC+∠C=180°,
∴2∠C=120°,
∴∠C=60°.
点评 本题主要考查了平行线的性质及判定定理,综合运用平行线的性质和判定定理是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
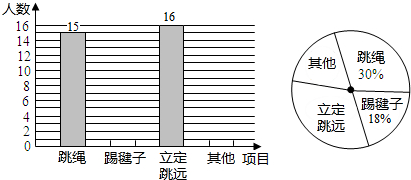
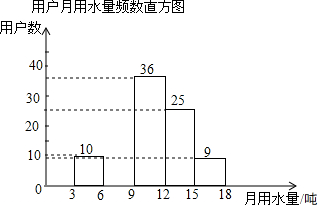 水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:| 用户月用水量频数分布表 | ||
| 平均用水量(吨) | 频数 | 频率 |
| 3~6吨 | 10 | 0.1 |
| 6~9吨 | m | 0.2 |
| 9~12吨 | 36 | 0.36 |
| 12~15吨 | 25 | n |
| 15~18吨 | 9 | 0.09 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
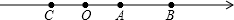 如图,点A、B、C都是数轴上的点,点B、C到点A的距离相等,若点A、B表示的数分别是2,$\sqrt{19}$,则点C表示的数为( )
如图,点A、B、C都是数轴上的点,点B、C到点A的距离相等,若点A、B表示的数分别是2,$\sqrt{19}$,则点C表示的数为( )| A. | 2-$\sqrt{19}$ | B. | $\sqrt{19}$-2 | C. | 4-$\sqrt{19}$ | D. | $\sqrt{19}$-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{9}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m2-m-6=(m+2)(m-3) | B. | (m+2)(m-3)=m2-m-6 | ||
| C. | x2+8x-9=(x+3)(m-3)+8x | D. | 18x3y2=3x3y2•6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com