
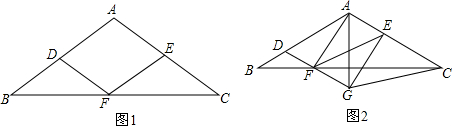
分析 (1)先证明四边形ADFE为平行四边形,再由等腰三角形的性质和已知条件证出AD=DF,即可得出四边形ADFE为菱形;
(2)先证明四边形ADFE为平行四边形,得出DF=AE,证明四边形AFGE是矩形,得出∠FAE=∠AEG=∠AFG=90°,再由等腰三角形的性质和已知条件得出BD=DF=AE=2,AD=EC=4,在Rt△ADF中,由三角函数求出AF,得出EG,在Rt△GEC中,根据勾股定理即可求出CG的长.
解答 解:(1)四边形ADFE为菱形,理由如下:如图1所示: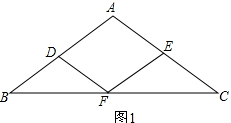
∵DF∥AC,
∴∠DFB=∠C,
∵EF∥AB,
∴四边形ADFE为平行四边形,
∵AB=AC,
∴∠B=∠C,
∴∠DFB=∠B,
∴DB=DF,
又∵D为AB中点,
∴DB=AD,
∴AD=DF,
∴四边形ADFE为菱形;
(2)如图2所示: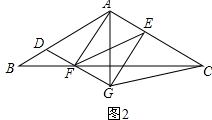 ∵DG∥AE,EF∥AD,
∵DG∥AE,EF∥AD,
∴四边形ADFE为平行四边形,
∴DF=AE,
∵DF=FG,
∴FG=AE,
∴四边形AFGE为平行四边形,
又∵AG=EF,
∴四边形AFGE为矩形,
∴∠FAE=∠AEG=∠AFG=90°,
又∵AB=AC,∠BAC=120°,
∴∠ABF=∠BAF=∠ACB=30°,
∴BD=DF=$\frac{1}{2}$AD=$\frac{1}{3}$AB,
∵AB=6,
∴BD=DF=AE=2,AD=EC=4,
在Rt△ADF中,AF=AD•cos30°=2$\sqrt{3}$,
∴EG=2$\sqrt{3}$,
在Rt△GEC中,∠GEC=90°,根据勾股定理得:
CG=$\sqrt{C{E}^{2}+E{G}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{3})^{2}}$=2$\sqrt{7}$.
点评 本题考查了菱形的判定与性质、矩形的判定、勾股定理、三角函数、等腰三角形的性质;本题有一定难度,特别是(2)中,需要证明四边形是矩形,运用三角函数和勾股定理才能得出结果.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
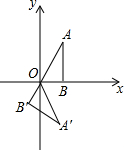 如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是(2,-2$\sqrt{3}$).
如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是(2,-2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
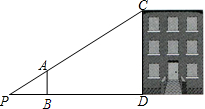 如图,是小彬利用标杆AB测量某建筑物高度的示意图,其中P,B,D在同一水平直线上,点P,A,C在同一直线上,AB⊥PD,CD⊥PD,测得标杆AB=1.5m,PB=2m,PB=6m,则该建筑物CD的高是6米.
如图,是小彬利用标杆AB测量某建筑物高度的示意图,其中P,B,D在同一水平直线上,点P,A,C在同一直线上,AB⊥PD,CD⊥PD,测得标杆AB=1.5m,PB=2m,PB=6m,则该建筑物CD的高是6米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
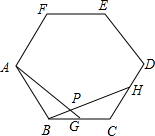 如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.(1)求证:△ABG≌△BCH;
如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.(1)求证:△ABG≌△BCH;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解全国中学生的视力情况,选择全面调查 | |
| B. | 为了了解一批袋装食品是否含有防腐剂,选择全面调查 | |
| C. | 为了检测某城市的空气质量,选择抽样调查 | |
| D. | 为了检测乘坐飞机的旅客是否携带违禁物品,选择抽样调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com