
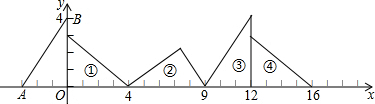
分析 先利用勾股定理得到AB=5,利用图形和旋转的性质可得到△OAB每三次旋转一个循环,并且每一个循环向前移动了12个单位,由于10=3×3+1,则可判断三角形⑩和三角形①的状态一样,且三角形⑩与三角形⑨的直角顶点相同,所以三角形⑩的直角顶点与坐标原点的距离为3×12=36.
解答 解:∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵对△OAB连续作如图所示的旋转变换,
∴△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,
∵10=3×3+1,
∴三角形⑩和三角形①的状态一样,则三角形⑩与三角形⑨的直角顶点相同,
∴三角形⑩的直角顶点的横坐标为3×12=36,纵坐标为0,
∴三角形⑩的直角顶点与坐标原点的距离为36.
故答案为36.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.解决本题的关键是确定△OAB连续作旋转变换后三角形的状态的变换规律.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$x(x-1)=21 | B. | $\frac{1}{2}$x(x+1)=21 | C. | x(x-1)=21 | D. | x(x+1)=21 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E且分别交PA、PB于点C,D,若PA=4,则△PCD的周长为( )
如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E且分别交PA、PB于点C,D,若PA=4,则△PCD的周长为( )| A. | 5 | B. | 7 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
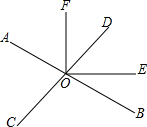 如图,直线AB、CD相交于点O,OE是∠BOD的平分线,如果∠AOC:∠AOD=7:11.
如图,直线AB、CD相交于点O,OE是∠BOD的平分线,如果∠AOC:∠AOD=7:11.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com