
 如图,要围成一个矩形花圃.花圃的一边利用足够长的墙,另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.
如图,要围成一个矩形花圃.花圃的一边利用足够长的墙,另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.分析 (1)设AB边的长为x米,则BC=32-2x,然后利用矩形的面积公式列出方程解答即可;
(2)求得矩形ABCD面积的二次函数解析式,利用二次函数的性质求最大值即可.
解答 解:(1)设AB=xm,则BC=(32-2x)m
由题意得:x(32-2x)=96
解得:x1=12,x2=4
当x1=12时,32-2x=8;
当x2=4时,32-2x=24;
答:AB=12m,BC=8m或AB=4m,BC=24米是可以围成.
(2)设:花圈的面积为s,AB=x,
s=x(32-2x),
s=-2x2+32x,
当x=-$\frac{32}{2×(-2)}$=8时,
s有最大值=-2×82+32×8=128,
∴当所围矩形花圈的AB=8m时,有最大面积128m2.
点评 此题主要考查的是二次函数的应用,一元二次方程的应用,掌握二次函数的性质、矩形的面积计算方法是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | $\sqrt{10}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数(1、2、1)恰好对应着(a+b)2的展开式a2+2ab+b2的系数;第四行的四个数恰好对应着(a+b)3=a3+3a2b+3ab2+b3的系数,根据数表中前五行的数字所反映的规律,回答:
如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数(1、2、1)恰好对应着(a+b)2的展开式a2+2ab+b2的系数;第四行的四个数恰好对应着(a+b)3=a3+3a2b+3ab2+b3的系数,根据数表中前五行的数字所反映的规律,回答:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
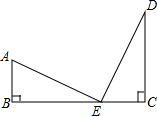 如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是( )
如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是( )| A. | 仅① | B. | 仅①③ | C. | 仅①③④ | D. | 仅①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com