
分析 (1)由抛物线y=ax2-2ax-3a(a<0)与x轴交于两点A、B,求得A点的坐标,作DF⊥x轴于F,根据平行线分线段成比例定理求得D的坐标,然后利用待定系数法法即可求得直线l的函数表达式.
(2)设点E(m,a(m+1)(m-3)),yAE=k1x+b1,利用待定系数法确定yAE=a(m-3)x+a(m-3),从而确定S△ACE=$\frac{1}{2}$(m+1)[a(m-3)-a]=$\frac{a}{2}$(m-$\frac{3}{2}$)2-$\frac{25}{8}$a,根据最值确定a的值即可;
(3)分以AD为对角线、以AC为边,AP为对角线、以AC为边,AQ为对角线三种情况利用矩形的性质确定点P的坐标即可.
解答 解:(1)令y=0,则ax2-2ax-3a=0,
解得x1=-1,x2=3
∵点A在点B的左侧,
∴A(-1,0),
如图1,作DF⊥x轴于F,
∴DF∥OC,
∴$\frac{OF}{OA}$=$\frac{CD}{AC}$,
∵CD=4AC,
∴$\frac{OF}{OA}$=$\frac{CD}{AC}$=4,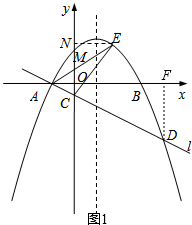
∵OA=1,
∴OF=4,
∴D点的横坐标为4,
代入y=ax2-2ax-3a得,y=5a,
∴D(4,5a),
把A、D坐标代入y=kx+b得$\left\{\begin{array}{l}{-k+b=0}\\{4k+b=5a}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=a}\\{b=a}\end{array}\right.$,
∴直线l的函数表达式为y=ax+a.
(2)如图1,过点E作EN⊥y轴于点N
设点E(m,a(m+1)(m-3)),yAE=k1x+b1,
则$\left\{\begin{array}{l}{a(m+1)(m-3)=m{k}_{1}+{b}_{1}}\\{0=-{k}_{1}+{b}_{1}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=a(m-3)}\\{{b}_{1}=a(m-3)}\end{array}\right.$,
∴yAE=a(m-3)x+a(m-3),M(0,a(m-3))
∵MC=a(m-3)-a,NE=m
∴S△ACE=S△ACM+S△CEM=$\frac{1}{2}$[a(m-3)-a]+$\frac{1}{2}$[a(m-3)-a]m=$\frac{1}{2}$(m+1)[a(m-3)-a]=$\frac{a}{2}$(m-$\frac{3}{2}$)2-$\frac{25}{8}$a,
∴有最大值-$\frac{25}{8}$a=$\frac{5}{4}$,
∴a=-$\frac{2}{5}$;
(3)令ax2-2ax-3a=ax+a,即ax2-3ax-4a=0,
解得x1=-1,x2=4,
∴D(4,5a),
∵y=ax2-2ax-3a,
∴抛物线的对称轴为x=1,
设P1(1,m),
①若AD是矩形的一条边,
由AQ∥DP知xD-xP=xA-xQ,可知Q点横坐标为-4,将x=-4带入抛物线方程得Q(-4,21a),
m=yD+yQ=21a+5a=26a,则P(1,26a),
∵四边形ADPQ为矩形,∴∠ADP=90°,
∴AD2+PD2=AP2,
∵AD2=[4-(-1)]2+(5a)2=52+(5a)2,
PD2=[4-(-1)]2+(5a)2=52+(5a)2,
∴[4-(-1)]2+(5a)2+(1-4)2+(26a-5a)2=(-1-1)2+(26a)2,
即a2=$\frac{1}{7}$,∵a<0,∴a=-$\frac{\sqrt{7}}{7}$,
∴P1(1,-$\frac{26\sqrt{7}}{7}$).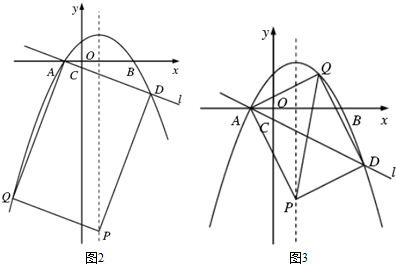
②若AD是矩形的一条对角线,
则线段AD的中点坐标为($\frac{3}{2}$,$\frac{5a}{2}$),Q(2,-3a),
m=5a-(-3a)=8a,则P(1,8a),
∵四边形ADPQ为矩形,∴∠APD=90°,
∴AP2+PD2=AD2,
∵AP2=[1-(-1)]2+(8a)2=22+(8a)2,
PD2=(4-1)2+(8a-5a)2=32+(3a)2,
AD2=[4-(-1)]2+(5a)2=52+(5a)2,
∴22+(8a)2+32+(3a)2=52+(5a)2,
解得a2=$\frac{1}{4}$,∵a<0,∴a=-$\frac{1}{2}$,
∴P2(1,-4).
综上可得,P点的坐标为P1(1,-4),P2(1,-$\frac{26\sqrt{7}}{7}$).
点评 本题是二次函数的综合题,考查了待定系数法求一次函数的解析式,二次函数图象上点的坐标特征,以及矩形的判定,根据平行线分线段成比例定理求得D的坐标是本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
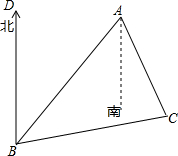 如图所示,B处在A处的南偏西45°方向上,C处在A处的南偏东30°方向,C处在B处的北偏东85°,求∠ACB是多少度?(提示:在三角形ABC中,∠BAC+∠ABC+∠ACB=180°)
如图所示,B处在A处的南偏西45°方向上,C处在A处的南偏东30°方向,C处在B处的北偏东85°,求∠ACB是多少度?(提示:在三角形ABC中,∠BAC+∠ABC+∠ACB=180°)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E是正方形ABCD内一点,连结AE、BE、DE.若AE=2,BE=$\sqrt{15}$,∠AED=135°,则正方形ABCD的面积为11+2$\sqrt{14}$.
如图,点E是正方形ABCD内一点,连结AE、BE、DE.若AE=2,BE=$\sqrt{15}$,∠AED=135°,则正方形ABCD的面积为11+2$\sqrt{14}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
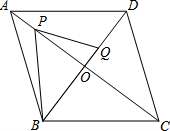 如图,已知菱形ABCD,对角线AC、BD相交于点O,AB=10,AC=16.点P在AO上,点Q在DO上,且AP=2OQ.
如图,已知菱形ABCD,对角线AC、BD相交于点O,AB=10,AC=16.点P在AO上,点Q在DO上,且AP=2OQ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com