Question

14．如图1，在△ABC中，∠ACB=90°，AC=3cm，BC=4cm，点D为AB中点，连结CD，动点P、Q从点C同时出发，点P沿BC边C→B→C以 2a cm/s的速度运动；点Q沿CA边C→A以 a cm/s的速度运动，当点Q到达点A时，两点停止运动，以CQ，CP为边作矩形CQMP，当矩形CQMP与△CDB重叠部分的图形是四边形使，设重叠部分图形的面积为y（cm²）．P、Q两点运动时间为t（s），在点P由C→B过程中，y与t的图象如图2所示．

（1）求a、m的值；
（2）求y与t的函数关系式，并写出t的取值范围．

Answer 1

分析 （1）根据图象可知，当t=$\frac{6}{5}$时，点M落在AB边上，根据△BPM∽△BCA，得到比例式，计算求出a，根据点D为AB中点，DQ∥BC，求出m；
（2）分0＜t≤$\frac{6}{5}$、$\frac{3}{2}$＜t＜2、2＜t＜3三种情况，根据相似三角形的性质解答即可．

解答 解（1）由图象得：当t=$\frac{6}{5}$时，点M落在AB边上，如图3所示，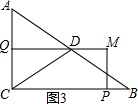
CP=$\frac{6}{5}$×2a=$\frac{12}{5}$a，CQ=$\frac{6}{5}$a，
∵△BPM∽△BCA，
∴$\frac{PM}{CA}$=$\frac{BP}{BC}$，即$\frac{\frac{6}{5}a}{3}$=$\frac{4-\frac{12}{5}a}{4}$，
解得：a=1，
根据题意得，当QM过点D时，t=m，如图4所示，
∵点D为AB中点，DQ∥BC，
∴点Q为AC中点
∴t=$\frac{3}{2}$，
∴m=$\frac{3}{2}$；
（2）当0＜t≤$\frac{6}{5}$时，如图5，CD与QM的交点是点G，
∵△CQG∽△ACB，
∴$\frac{CQ}{AC}$=$\frac{QG}{CB}$，即$\frac{t}{3}$=$\frac{QG}{4}$，
整理得：QG=$\frac{4}{3}$t，
∴S_△CQG=$\frac{1}{2}$•t•$\frac{4}{3}$t=$\frac{2}{3}$t²，
∴y=2t²-$\frac{2}{3}$t²=$\frac{4}{3}$t^2，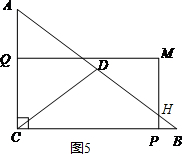
当$\frac{3}{2}$＜t＜2时，如图5，PM与BD交点是H，
∴△BHP∽△BAC，
∴$\frac{BP}{BC}$=$\frac{HP}{AC}$，即$\frac{BP}{4}$=$\frac{HP}{3}$，
∴HP=$\frac{3}{4}$BP，
∴y=S_△BCD-S_△BHP=3-$\frac{1}{2}$BP•$\frac{3}{4}$BP=3-$\frac{3}{8}$BP²=3-$\frac{3}{8}$（4-2t）²=-$\frac{3}{2}$t²+6t-3；
当2＜t＜3时，同理得到y=3-$\frac{3}{8}$（2t-4）²=-$\frac{3}{2}$t²+6t-3．

点评 本题考查的是动点问题的函数图象、相似三角形的判定和性质，正确读懂函数图象、正确运用相似三角形的判定定理和性质定理是解题的关键．