

���� ��1�����ݡ�DAE=��BAC���õ���BAD=��CAE���Ƴ���ABD�ա�ACE������ȫ�������ε����ʵõ���ACE=��ABC=60�㣬���ݵõ����ۣ�
��2���ɡ�BAC=��DAE���õ���BAD=��CAE���Ƴ���ABD�ա�ACE������ȫ�������ε����ʵõ���B=��ACE�����ǵõ���B+��ACB=��ACE+��ACB��֤�á�B+��ACB=��DCE=�Ϧ£����ɵõ����ۣ�
���ɡ�DAE=��BAC���õ���DAB=��EAC���Ƴ���ABD�ա�ACE������ȫ�������ε����ʵõ���ADB=��AEC�����߶�AE���߶�CB�ཻ�ڵ�F�����ǵõ���DFA=��EFC�����ɵõ����ۣ�
��� �⣺��1���ߡ�DAE=��BAC��
���BAD=��CAE��
�ڡ�ABD���ACE�У�$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAE}\\{AD=AE}\end{array}\right.$��
���ABD�ա�ACE��
���ACE=��ABC=60�㣬
���=120�㣬
�ʴ�Ϊ��120�㣻
��2���٦�+��=180�㣬
���ɣ��ߡ�BAC=��DAE��
���BAC-��DAC=��DAE-��DAC��
����BAD=��CAE��
�ڡ�ABD���ACE�У�$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAE}\\{AD=AE}\end{array}\right.$��
���ABD�ա�ACE��
���B=��ACE��
���B+��ACB=��ACE+��ACB��
���B+��ACB=��DCE=�Ϧ£�
�ߦ�+��B+��ACB=180�㣬
���+��=180�㣬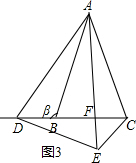
��ͼ����ȷ����=�£�
�ߡ�DAE=��BAC��
���DAE-��BAE=��BAC-��BAE��
����DAB=��EAC��
�ڡ�ABD���ACE�У�$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAE}\\{AD=AE}\end{array}\right.$��
���ABD�ա�ACE��
���ADB=��AEC��
���߶�AE���߶�CB�ཻ�ڵ�F��
���DFA=��EFC��
�ߡ�DAF+��DFA+��ADF=��ECF+��EFC+��AEC=180�㣬
���DAF=��ECF��
���=�£�
���� ������Ҫ�����˵���ֱ�������ε����ʡ�ȫ�������ε��ж��������ʵȼ���֪ʶ�㼰��Ӧ�����⣻Ӧ�ι����յ���ֱ�������ε����ʡ�ȫ�������ε��ж��������ʵȼ���֪ʶ�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��n | B�� | m��n | C�� | m=n | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
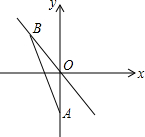 ��ͼ��A��0��-$\sqrt{2}$������BΪֱ��y=-x��һ���㣬���߶�AB���ʱ����B������Ϊ��������
��ͼ��A��0��-$\sqrt{2}$������BΪֱ��y=-x��һ���㣬���߶�AB���ʱ����B������Ϊ��������| A�� | ��0��0�� | B�� | ��1��-1�� | C�� | ��$\frac{1}{2}$��-$\frac{1}{2}$�� | D�� | ��$\frac{\sqrt{2}}{2}$��-$\frac{\sqrt{2}}{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-x=0 | B�� | x2-7x+6=0 | C�� | 2x2-3x-5=0 | D�� | 3x2+2x-5=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����AOB=90�㣬��PΪ��AOB��һ�㣮
��ͼ����AOB=90�㣬��PΪ��AOB��һ�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com