
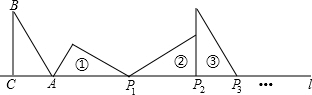
 如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此顺序继续旋转,得到点P2016,则AP2016=( )
如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此顺序继续旋转,得到点P2016,则AP2016=( )| A. | 2016+671$\sqrt{3}$ | B. | 2016+672$\sqrt{3}$ | C. | 2017+672$\sqrt{3}$ | D. | 2016+673$\sqrt{3}$ |
分析 利用题意得AP3=3+$\sqrt{3}$,则易得AP6=2(3+$\sqrt{3}$),AP9=3(3+$\sqrt{3}$),则三角形旋转三次一个循环,一个循环3+$\sqrt{3}$,然后由2016=3×672即可得到AP2016的长度.
解答 解:∵AP1=2,AP2=2+$\sqrt{3}$,AP3=3+$\sqrt{3}$,
∴AP6=2(3+$\sqrt{3}$),
AP9=3(3+$\sqrt{3}$),
而2016=3×672,
∴AP2016=672(3+$\sqrt{3}$)=2016+672$\sqrt{3}$.
故选B.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了规律型问题的解决方法.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
| A. | 表面积一定相等 | B. | 体积一定相等 | C. | 侧面积一定相等 | D. | 底面积一定相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
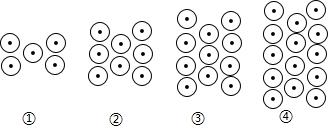
| A. | 2998 | B. | 3001 | C. | 3002 | D. | 3005 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com